
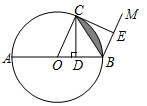
 如图,⊙O的直径AB=4,C是⊙O上一点,连接OC.过点C作CD⊥AB,垂足为D,过点B作BM∥OC,在射线BM上取点E,使BE=BD,连接CE.
如图,⊙O的直径AB=4,C是⊙O上一点,连接OC.过点C作CD⊥AB,垂足为D,过点B作BM∥OC,在射线BM上取点E,使BE=BD,连接CE.分析 (1)图中阴影部分的面积=扇形的面积-三角形的面积;
(2)欲证明CE是⊙O的切线,只需推知∠OCE=90°即可.
解答 解:(1)∵OC=OB,∠COB=60°,
∴△BOC是等边三角形,∴S△BOC=$\frac{\sqrt{3}}{4}$•22=$\sqrt{3}$
S阴=S扇形OBC-S△BOC=$\frac{60•π•{2}^{2}}{360}$-$\frac{\sqrt{3}}{4}$•22=$\frac{2π}{3}-\sqrt{3}$;
(2)证明:∵BM∥OC
∴∠OCB=∠CBE.
∵OC=OB
∴∠OCB=∠OBC
∴∠OBC=∠CBE
又BD=BE,BC=BC
△CBD≌△CBE
∴∠CEB=∠CDB=90°.
∵BM∥OC,
∴∠OCE+∠CEB=180°,
∴∠OCE=180°-∠CEB=180°-90°=90°,
即OC⊥CE,
∴CE是⊙O的切线.
点评 本题考查了切线的判定、扇形的面积公式、等边三角形的判定和性质等知识,解题的关键是熟练掌握切线的判定方法,学会用分割法求阴影部分面积,属于中考常考题型.


科目:初中数学 来源: 题型:选择题
| 年龄/岁 | 12 | 13 | 14 | 15 |
| 频数 | 6 | 9 | 15-a | a |
| A. | 平均数 | B. | 众数 | C. | 方差 | D. | 中位数 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
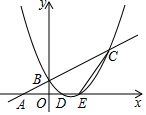 已知:如图一次函数y=$\frac{1}{2}$x+1的图象与x轴交于点A,与y轴交于点B;二次函数y=$\frac{1}{2}$x2+bx+c的图象与一次函数y=$\frac{1}{2}$x+1的图象交于B、C两点,与x轴交于D、E两点且D点坐标为(1,0)
已知:如图一次函数y=$\frac{1}{2}$x+1的图象与x轴交于点A,与y轴交于点B;二次函数y=$\frac{1}{2}$x2+bx+c的图象与一次函数y=$\frac{1}{2}$x+1的图象交于B、C两点,与x轴交于D、E两点且D点坐标为(1,0)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (2,4) | B. | (2,3) | C. | (-1,6) | D. | (-$\frac{1}{2}$,3) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
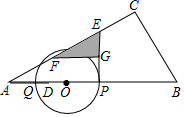 如图,在△ABC中,∠C=90°,∠CAB=30°,AB=10,点D在线段AB上,AD=2.点P,Q以相同的速度从D点同时出发,点P沿DB方向运动,点Q沿DA方向到点A后立刻以原速返回向点B运动.以PQ为直径构造⊙O,过点P作⊙O的切线交折线AC-CB于点E,将线段EP绕点E顺时针旋转60°得到EF,过F作FG⊥EP于G,当P运动到点B时,Q也停止运动,设DP=m.
如图,在△ABC中,∠C=90°,∠CAB=30°,AB=10,点D在线段AB上,AD=2.点P,Q以相同的速度从D点同时出发,点P沿DB方向运动,点Q沿DA方向到点A后立刻以原速返回向点B运动.以PQ为直径构造⊙O,过点P作⊙O的切线交折线AC-CB于点E,将线段EP绕点E顺时针旋转60°得到EF,过F作FG⊥EP于G,当P运动到点B时,Q也停止运动,设DP=m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com