
【题目】若a、b互为相反数,b、C互为倒数,并且m的立方等于它本身
(1)求![]() +ac值;
+ac值;
(2)若a>1,且m<0,S=|2a-3b|-2|b-m|-|b+![]() |,求2a-S的值.
|,求2a-S的值.
(3)若m≠0,试讨论:x为有理数时|x+m|-|x-m|是否存在最大值?若存在,求出这个最大值:若不存在,请说明理由.
【答案】(1)-1;(2)![]() ;(3)2.
;(3)2.
【解析】
(1)先根据a、b互为相反数,b、c互为倒数,得出a+b=0,bc=1,再代入所求代数式进行计算;
(2)根据a>1及m的立方等于它本身把S进行化简,再代入所求代数式进行计算;
(3)根据若![]() 可知
可知![]() ,①当m=1时,代入
,①当m=1时,代入![]() ,再根据绝对值的性质去掉绝对值符号,求出代数式的值,②同理,当m=-1时代入所求代数式,再根据绝对值的性质去掉绝对值符号,求出代数式的值,即可.
,再根据绝对值的性质去掉绝对值符号,求出代数式的值,②同理,当m=-1时代入所求代数式,再根据绝对值的性质去掉绝对值符号,求出代数式的值,即可.
1)∵a、b互为相反数,b、C互为倒数
∴a+b=0,be=1,
∴ac=-1(3分)
∴![]() +ac=0-1=-1(4分)
+ac=0-1=-1(4分)
(2)∵a>1
∴b<-1,2a-3b>0,b+![]() <0(5分)
<0(5分)
∵m的立方等于它本身,且m<0
∴m=-1,b-m=b+1<0(6分)
∴S=2a-3b+2b+2+b+![]() =2a+
=2a+![]()
∴2a-S=-![]() (7分)
(7分)
3)若m≠0,此时m=±1(8分)
①若m=1,则|x+m|-|x-m|=|x+1|-|x-1|
当x≤-1时
|x+1|-|x-1|=-x-1+x-1=-2
当-1<x≤1时
|x+1|-|x-1|=x+1+x-1=2x
当x>1时
|x+1|-|x-1|=x+1-x+1=2
当x为有理数时,存在最大值为2;(11分)
②若m=-1
同理可得:当x为有理数时,存在最大值为2.(12分)
综上所述,当m=±1,x为有理数时,|x+m|-|x-m|存在最大值为2.


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,∠A=36°,DE垂直平分AB交AC于D,交AB于E,下列论述错误的是( )

A. BD平分∠ABC B. D是AC的中点
C. AD=BD=BC D. △BDC的周长等于AB+BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一应用题:“李老师存了一个两年的定期储蓄5000元,到期后扣除20%的利息税能取5176元,求这种储蓄的年利率是多少?”四位同学都是设这种储蓄的年利率是x,可他们列出的方程却不同,下列列出的方程中正确的是()
A. 5000(1+x×2×20%)=5176 B. 5000(1+2x)×80%=5176
C. 5000+5000x×2×80%=5176 D. 5000+5000x×80%=5176
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C,P是 ![]() 上两点,AB=13,AC=5.
上两点,AB=13,AC=5. 
(1)如图(1),若点P是 ![]() 的中点,求PA的长;
的中点,求PA的长;
(2)如图(2),若点P是 ![]() 的中点,求PA的长.
的中点,求PA的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)分解因式:![]() (2)分解因式: 9a2(x—y)+4b2(y—x)
(2)分解因式: 9a2(x—y)+4b2(y—x)
(3)分解因式:(x2+y2)2-4x2y2 (4)利用分解因式计算求值:2662-2342
(5)利用分解因式计算求值:已知x-3y=-1,xy=2,求x3y-6x2y2+9xy3的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=x+1分别与x轴、y轴相交于点A、B,以点A为圆心、AB长为半径画弧交x轴于点A1,再过点A1作x轴的垂线交直线于点B1,以点A为圆心、AB1长为半径画弧交x轴于点A2……按此做法进行下去,则点A8的坐标是________.
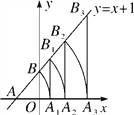
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径为AB,点C在圆周上(异于A,B),AD⊥CD. 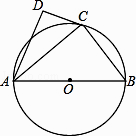
(1)若BC=3,AB=5,求AC的值;
(2)若AC是∠DAB的平分线,求证:直线CD是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家超市以相同的价格出售同样的商品,但为了吸引顾客,各自推出不同的优惠方案:在甲超市累计购买商品超过400元后,超过部分按原价七折优惠;在乙超市购买商品只按原价的八折优惠;设顾客累计购物![]() 元(
元(![]() )
)
(1)用含![]() 的代数式分别表示顾客在两家超市购买所付的费用。
的代数式分别表示顾客在两家超市购买所付的费用。
(2)当![]() 时,试比较顾客到哪家超市购物更加优惠。
时,试比较顾客到哪家超市购物更加优惠。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com