已知:二次函数y=ax2+bx-2的图象经过点(1,0),一次函数图象经过原点和点(1,-b),其中a>b>0且a、b为实数.
(1)求一次函数的表达式(用含b的式子表示);
(2)试说明:这两个函数的图象交于不同的两点;
(3)设(2)中的两个交点的横坐标分别为x1、x2,求|x1-x2|的范围.
【答案】
分析:(1)一次函数经过原点,说明这个一次函数是正比例函数,将点(1,-b)的坐标代入,即可求得这个一次函数的表达式.
(2)将点(1,0)代入抛物线的解析式中,可得到a、b的关系式,用b替换掉a后联立一次函数的解析式,可得到一个关于x的一元二次方程,判断方程的根的判别式是否大于0即可.
(3)由题意知:x
1、x
2是(2)题所得一元二次方程的两个实数根,根据韦达定理即可求得|x
1-x
2|的表达式,然后根据a、b的符号以及(2)题所得a、b的关系式即可得到|x
1-x
2|的取值范围.
解答:解:(1)∵一次函数过原点,
∴设一次函数的解析式为y=kx;
∵一次函数过(1,-b),
∴y=-bx.(3分)
(2)∵y=ax
2+bx-2过(1,0),即a+b=2,(4分)
∴b=2-a.
由

,得:(5分)
ax
2+bx-2=-bx,
∴ax
2+(2-a)x-2=-(2-a)x,
∴ax
2+2(2-a)x-2=0①;
∵△=4(2-a)
2+8a=16-16a+4a
2+8a=4(a
2-2a+1)+12=4(a-1)
2+12>0,
∴方程①有两个不相等的实数根,
∴方程组有两组不同的解,
∴两函数图象有两个不同的交点.(6分)
(3)∵两交点的横坐标x
1、x
2分别是方程①的解,
∴x
1+x
2=-
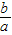
,∴x
1+x
2=-
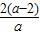
,
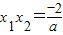
;
∴
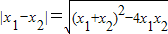
=
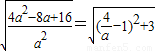
;
(或由求根公式得出)(8分)
∵a>b>0,a+b=2,
∴2>a>1;
令函数
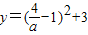
,
∵在1<a<2时,y随a增大而减小.
∴
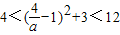
;(9分)
∴
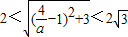
,
∴
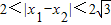
.(10分)
点评:此题主要考查的是函数图象交点、根与系数的关系、二次函数的性质以及不等式的应用,能够结合二次函数的性质来解不等式是解决(3)题的关键.

 ,得:(5分)
,得:(5分)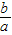 ,∴x1+x2=-
,∴x1+x2=-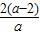 ,
,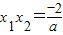 ;
;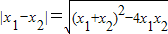 =
=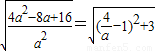 ;
;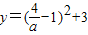 ,
,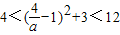 ;(9分)
;(9分)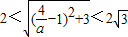 ,
,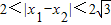 .(10分)
.(10分)

 已知:二次函数的表达式为y=2x2+4x-1.
已知:二次函数的表达式为y=2x2+4x-1.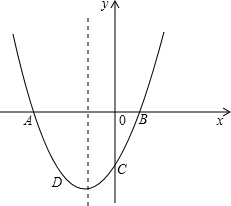 交于点C,点D(-2,-3)在抛物线上.
交于点C,点D(-2,-3)在抛物线上.