
 盏路灯(可以看成点C),已知点C与点A的铅垂距离CD=9m,水平距离AD=6.4m(图中CD⊥AD,AD⊥AB).
盏路灯(可以看成点C),已知点C与点A的铅垂距离CD=9m,水平距离AD=6.4m(图中CD⊥AD,AD⊥AB). 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案科目:初中数学 来源: 题型:
 盏路灯(可以看成点C),已知点C与点A的铅垂距离CD=9m,水平距离AD=6.4m(图中CD⊥AD,AD⊥AB).
盏路灯(可以看成点C),已知点C与点A的铅垂距离CD=9m,水平距离AD=6.4m(图中CD⊥AD,AD⊥AB).查看答案和解析>>
科目:初中数学 来源: 题型:
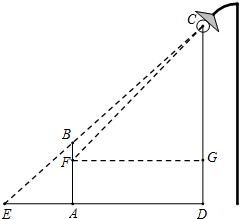
 (2013•大连一模)如图,为了测量某建筑物CD的高度,测量人员先在地面上用测角仪AE自A处测得建筑物顶部C的仰角是30°,然后在水平地面上向建筑物前进42米,此时自B处测得建筑物顶部C的仰角是60°.已知测角仪的高度始终是1.5米,则该建筑物CD的高度约为
(2013•大连一模)如图,为了测量某建筑物CD的高度,测量人员先在地面上用测角仪AE自A处测得建筑物顶部C的仰角是30°,然后在水平地面上向建筑物前进42米,此时自B处测得建筑物顶部C的仰角是60°.已知测角仪的高度始终是1.5米,则该建筑物CD的高度约为| 2 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在水平地面点A处有一网球发射器向空中发射网球,网球飞行路线是一条抛物线,在地面上落点为B.有人在直线AB上点C(靠点B一侧)竖直向上摆放无盖的圆柱形桶,试图让网球落入桶内.已知AB=4米,AC=3米,网球飞行最大高度OM=5米,圆柱形桶的直径为0.5米,高为0.3米(网球的体积和圆柱形桶的厚度忽略不计).以AB所在直线为x轴,OM所在直线为y轴建立平面直角坐标系.
如图,在水平地面点A处有一网球发射器向空中发射网球,网球飞行路线是一条抛物线,在地面上落点为B.有人在直线AB上点C(靠点B一侧)竖直向上摆放无盖的圆柱形桶,试图让网球落入桶内.已知AB=4米,AC=3米,网球飞行最大高度OM=5米,圆柱形桶的直径为0.5米,高为0.3米(网球的体积和圆柱形桶的厚度忽略不计).以AB所在直线为x轴,OM所在直线为y轴建立平面直角坐标系.查看答案和解析>>
科目:初中数学 来源:2011年浙江省宁波市慈溪市中考数学模拟试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com