
·ÖĪö £Ø1£©ČĪČ”Į½øö·ūŗĻŅŖĒóµÄŹż“śČėĢāÄæÖŠµÄŹ½×Ó£¬µČŹ½Į½±ßµÄ½į¹ūæ“ŹĒ·ńŅ»ÖĀ¼“æɽā“š±¾Ģā£»
£Ø2£©·Ö±š¶ŌµČŹ½Į½±ßÕ¹æŖ»Æ¼ņ£¬æ“×īŗóµÄ½į¹ūŹĒ·ńĻąµČ£¬¼“æɽā“š±¾Ģā£®
½ā“š ½ā£ŗ£Ø1£©¢Łµ±a=1£¬b=1Ź±£¬
£Ø$\frac{a}{b}$£©2+$\frac{b-a}{b}$=$£Ø\frac{1}{1}£©^{2}+\frac{1-1}{1}=1$£¬$\frac{a}{b}$+£Ø$\frac{b-a}{b}$£©2=$\frac{1}{1}+£Ø\frac{1-1}{1}£©^{2}$=1£¬
”ą£Ø$\frac{a}{b}$£©2+$\frac{b-a}{b}$=$\frac{a}{b}$+£Ø$\frac{b-a}{b}$£©2³ÉĮ¢£¬
¹Ź“š°øĪŖ£ŗ1£¬1£¬³ÉĮ¢£»
¢Śµ±a=1£¬b=2Ź±£¬
£Ø$\frac{a}{b}$£©2+$\frac{b-a}{b}$=$£Ø\frac{1}{2}£©^{2}+\frac{2-1}{2}=\frac{3}{4}$£¬$\frac{a}{b}$+£Ø$\frac{b-a}{b}$£©2=$\frac{1}{2}+£Ø\frac{2-1}{2}£©^{2}$=$\frac{3}{4}$£¬
”ą£Ø$\frac{a}{b}$£©2+$\frac{b-a}{b}$=$\frac{a}{b}$+£Ø$\frac{b-a}{b}$£©2³ÉĮ¢£¬
¹Ź“š°øĪŖ£ŗ1£¬2£¬³ÉĮ¢£»
£Ø2£©”ß${£Ø\frac{a}{b}£©^2}+\frac{b-a}{b}=\frac{a^2}{b^2}+\frac{b-a}{b}=\frac{{{a^2}+b£Øb-a£©}}{b^2}=\frac{{{a^2}-ab+{b^2}}}{b^2}$£¬
$\frac{a}{b}+{£Ø\frac{b-a}{b}£©^2}=\frac{a}{b}+\frac{{{b^2}-2ab+{a^2}}}{b^2}=\frac{{{a^2}-ab+{b^2}}}{b^2}$£¬
”ąµČŹ½${£Ø\frac{a}{b}£©^2}+\frac{b-a}{b}$=$\frac{a}{b}+{£Ø\frac{b-a}{b}£©^2}$³ÉĮ¢£®
µćĘĄ ±¾Ģāæ¼²é·ÖŹ½µÄ»ģŗĻŌĖĖć£¬½ā“š±¾ĢāµÄ¹Ų¼üŹĒĆ÷Č·ĢāŅā£¬ÕŅ³öĖłĒóĪŹĢāŠčŅŖµÄĢõ¼ž£®


 ĢģĢģĻņÉĻŅ»±¾ŗĆ¾ķĻµĮŠ“š°ø
ĢģĢģĻņÉĻŅ»±¾ŗĆ¾ķĻµĮŠ“š°ø Š”ѧɜ10·ÖÖÓÓ¦ÓĆĢāĻµĮŠ“š°ø
Š”ѧɜ10·ÖÖÓÓ¦ÓĆĢāĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | єȔøĆŠ£50ĆūÅ®Éś | B£® | єȔøĆŠ£50ĆūÄŠÉś | ||
| C£® | єȔøĆŠ£Ņ»øö°ą¼¶µÄѧɜ | D£® | Ė껜єȔøĆŠ£50Ćūѧɜ |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
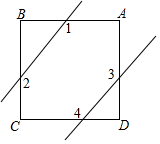 ČēĶ¼£¬Õż·½ŠĪABCDÖŠ£¬½ŲČ„”ĻB”¢”ĻDŗ󣬔Ļ1”¢”Ļ2”¢”Ļ3”¢”Ļ4µÄŗĶĪŖ540”ć£®
ČēĶ¼£¬Õż·½ŠĪABCDÖŠ£¬½ŲČ„”ĻB”¢”ĻDŗ󣬔Ļ1”¢”Ļ2”¢”Ļ3”¢”Ļ4µÄŗĶĪŖ540”ć£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
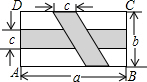 ČēĶ¼£¬ŌŚ¾ŲŠĪABCDÖŠ£¬ŗįĻņŅõÓ°²æ·ÖŹĒ¾ŲŠĪ£¬ĮķŅ»ŅõÓ°²æ·ÖŹĒĘ½ŠŠĖıߊĪ£¬ŅĄÕÕĶ¼ÖŠ±ź×¢µÄŹż¾Ż£¬¼ĘĖćĶ¼ÖŠæհײæ·ÖµÄĆ껿£¬ĘäĆ껿ŹĒ£Ø””””£©
ČēĶ¼£¬ŌŚ¾ŲŠĪABCDÖŠ£¬ŗįĻņŅõÓ°²æ·ÖŹĒ¾ŲŠĪ£¬ĮķŅ»ŅõÓ°²æ·ÖŹĒĘ½ŠŠĖıߊĪ£¬ŅĄÕÕĶ¼ÖŠ±ź×¢µÄŹż¾Ż£¬¼ĘĖćĶ¼ÖŠæհײæ·ÖµÄĆ껿£¬ĘäĆ껿ŹĒ£Ø””””£©| A£® | bc-ab+ac+c2 | B£® | a2+ab+bc-ac | C£® | ab-bc-ac+c2 | D£® | bc-ab+ac+c2 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | 1£¬2£¬3£¬4 | B£® | 6£¬5£¬10£¬15 | C£® | 3£¬2£¬6£¬4 | D£® | 15£¬3£¬4£¬10 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
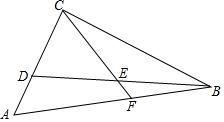 ŅŃÖŖ£ŗČēĶ¼£¬ŌŚRt”÷ABCÖŠ£¬”ĻACB=90”ć£¬µćDŌŚ±ßACÉĻ£¬µćEŹĒBDµÄÖŠµć£¬CEµÄŃÓ³¤Ļß½»±ßABÓŚµćF£¬ĒŅ”ĻCED=”ĻA£®
ŅŃÖŖ£ŗČēĶ¼£¬ŌŚRt”÷ABCÖŠ£¬”ĻACB=90”ć£¬µćDŌŚ±ßACÉĻ£¬µćEŹĒBDµÄÖŠµć£¬CEµÄŃÓ³¤Ļß½»±ßABÓŚµćF£¬ĒŅ”ĻCED=”ĻA£®²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com