
【题目】已知抛物线C1:y=ax2﹣4ax﹣5的开口向上.
(1)当a=1时,求抛物线与x轴的交点坐标;
(2)试说明抛物线C1一定经过两个定点,并求出这两个定点的坐标;
(3)将抛物线C1沿(2)所求的两个定点所在直线翻折,得到抛物线C2,
①写出抛物线C2的表达式;
②当抛物线C2的顶点到x轴的距离为2,求a的值.
【答案】(1)抛物线与x轴的交点坐标为(﹣1,0)或(5,0);(2)抛物线C1一定经过两个定点(0,﹣5),(4,﹣5);(3)①抛物线C2解析式为y=﹣ax2+4ax﹣5,②a=![]() 或
或![]() .
.
【解析】
(1)将a=1代入函数解析式,即可求出函数的解析式,然后令y=0,求出x的值即可解决.
(2)将解析式化成两部分,一部分为常数项,另一部分进行因式分解写成几个因式相乘的形式,观察解析式的特征,即可解决问题.
(3)①根据翻折的性质,抛物线开口方向相反,但对称轴没有发生变化,根据此可以得到抛物线C2解析式为:y=﹣ax2+4ax﹣5,②根据二次函数的性质,可知y=2或y=-2,对称轴未发生变化,x=2,将两者分别代入,求出a的值即可.
(1)当a=1时,抛物线解析式为y=x2﹣4x﹣5=(x﹣2)2﹣9,
∴对称轴为x=2;
∴当y=0时,x﹣2=3或﹣3,即x=﹣1或5;
∴抛物线与x轴的交点坐标为(﹣1,0)或(5,0);
(2)抛物线C1解析式为:y=ax2﹣4ax﹣5,
整理得:y=ax(x﹣4)﹣5;
∵当ax(x﹣4)=0时,y恒定为﹣5;
∴抛物线C1一定经过两个定点(0,﹣5),(4,﹣5);
(3)①这两个点连线为y=﹣5;
将抛物线C1沿y=﹣5翻折,得到抛物线C2,开口方向变了,但是对称轴没变;
∴抛物线C2解析式为:y=﹣ax2+4ax﹣5,
②抛物线C2的顶点到x轴的距离为2,
则x=2时,y=2或者﹣2;
当y=2时,2=﹣4a+8a﹣5,解得,a=![]() ;
;
当y=﹣2时,﹣2=﹣4a+8a﹣5,解得,a=![]() ;
;
∴a=![]() 或
或![]() .
.


 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90°,点A,C的坐标分别为A(﹣3,0),C(1,0),tan∠BAC=![]() .
.
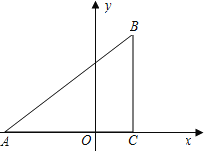
(1)求过点A,B的直线的函数表达式;
(2)在x轴上找一点D,连接BD,使得△ADB与△ABC相似(不包括全等),并求点D的坐标;
(3)在(2)的条件下,如P,Q分别是AB和AD上的动点,连接PQ,设AP=DQ=m,问是否存在这样的m使得△APQ与△ADB相似?如存在,请求出的m值;如不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】高考英语听力测试期间,需要杜绝考点周围的噪音。如图,点A是某市一高考考点,在位于A考点南偏西15°方向距离125米的![]() 点处有一消防队。在听力考试期间,消防队突然接到报警电话,告知在位于C点北偏东75°方向的F点处突发火灾,消防队必须立即赶往救火。已知消防车的警报声传播半径为100米,若消防车的警报声对听力测试造成影响,则消防车必须改道行驶。试问:消防车是否需要改道行驶?说明理由.(
点处有一消防队。在听力考试期间,消防队突然接到报警电话,告知在位于C点北偏东75°方向的F点处突发火灾,消防队必须立即赶往救火。已知消防车的警报声传播半径为100米,若消防车的警报声对听力测试造成影响,则消防车必须改道行驶。试问:消防车是否需要改道行驶?说明理由.(![]() 取1.732)
取1.732)
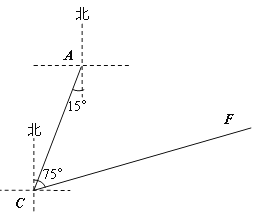
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司试销一种成本单价为50元/件的新产品,规定试销时销售单价不低于成本单价,又不高于80元/件,经试销调查,发现销售量y(件)与销售单价x(元/件)可近似看作一次函数y=kx+b的关系(如图所示)
(I)根据图象,求一次函数y=kx+b的解析式,并写出自变量x的取值范围;
(Ⅱ)该公司要想每天获得最大的利润,应把销售单价定为多少?最大利润值为多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点P(x0,m),Q(1,n)在二次函数y=(x+a)(x﹣a﹣1)(a≠0)的图象上,且m<n下列结论:①该二次函数与x轴交于点(﹣a,0)和(a+1,0);②该二次函数的对称轴是x=![]() ; ③该二次函数的最小值是(a+2)2; ④0<x0<1.其中正确的是_____.(填写序号)
; ③该二次函数的最小值是(a+2)2; ④0<x0<1.其中正确的是_____.(填写序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校初三学生上周末使用手机的情况(选项:A.聊天;B.学习;C.购物;D.游戏;E.其他),随机抽查了该校初三若干名学生,对其上周末使用手机的情况进行统计(每个学生只选一个选项),绘制了统计表和条形统计图.
选项 | 人数 | 频率 |
A | 15 | 0.3 |
B | 10 | m |
C | 5 | 0.1 |
D | n | |
E | 5 | 0.1 |
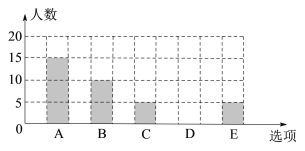
根据以上信息回答下列问题:
(1)这次调查的样本容量是 ;
(2)统计表中m= ,n= ,补全条形统计图;
(3)若该校初三有540名学生,请估计该校初三学生上周末利用手机学习的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以AB为直径的半圆O内有一条弦AC,点E是弦AC的中点,连接BE,并延长交半圆O于点D,若OB=2,OE=1,则∠CDE的度数是_______________.
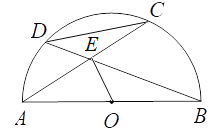
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() ,顶点为A,且经过点
,顶点为A,且经过点![]() ,点
,点![]() .
.
(1)求抛物线的解析式;
(2)如图1,直线AB与x轴相交于点M,y轴相交于点E,抛物线与y轴相交于点F,在直线AB上有一点P,若∠OPM=∠MAF,求△POE的面积;
(3)如图2,点Q是折线A﹣B﹣C上一点,过点Q作QN∥y轴,过点E作EN∥x轴,直线QN与直线EN相交于点N,连接QE,将△QEN沿QE翻折得到△QEN1,若点N1落在x轴上,请直接写出Q点的坐标.
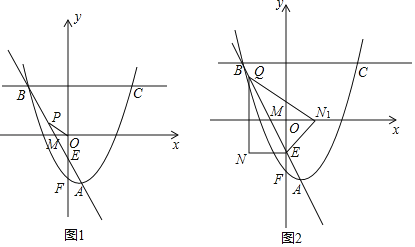
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A、B两点的坐标分别为(4,0)和(0,3),动点P从点A出发,以每秒2个长度单位的速度沿AO向O运动,在点P出发的同时,动直线EF从x轴出发,以每秒1个长度单位沿y轴方向向上平移,分别与y轴、线段AB交于EP、FP.设运动时间为ts(0<t≤2).
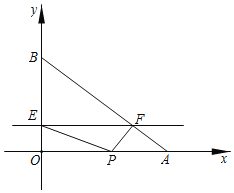
(1)在运动过程中,是否存在某一时刻t,使得△EOP与△AOB相似?若存在,请求出所有符合题意的t的值;若不存在,请说明理由.
(2)若△PEF是等腰三角形,求t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com