
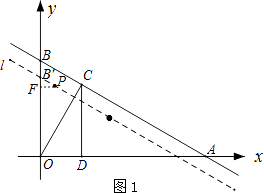
【题目】如图,已知点 ![]() ,经过A、B的直线l以每秒1个单位的速度向下作匀速平移运动,与此同时,点P从点B出发,在直线l上以每秒1个单位的速度沿直线l向右下方向作匀速运动.设它们运动的时间为t秒.
,经过A、B的直线l以每秒1个单位的速度向下作匀速平移运动,与此同时,点P从点B出发,在直线l上以每秒1个单位的速度沿直线l向右下方向作匀速运动.设它们运动的时间为t秒.
(1)用含t的代数式表示点P的坐标;
(2)过O作OC⊥AB于C,过C作CD⊥x轴于D,问:t为何值时,以P为圆心、1为半径的圆与直线OC相切?并说明此时⊙P与直线CD的位置关系.
【答案】
(1)
解:作PF⊥y轴于F.
∵点 ![]() ,
,
∴∠BAO=30°.
在直角三角形PFB′中,PB′=t,∠B′PF=30°,
则B′F= ![]() ,PF=
,PF= ![]() .
.
又BB′=t,
∴OF=OB﹣BB′﹣B′F=6﹣t﹣ ![]() =6﹣
=6﹣ ![]() t,
t,
则P点的坐标为( ![]() ,6﹣
,6﹣ ![]() t).
t).
(2)
解:此题应分为两种情况:
①当⊙P和OC第一次相切时,
设直线B′P与OC的交点是M,
根据题意,知∠BOC=∠BAO=30°.
则B′M= ![]() OB′=3﹣
OB′=3﹣ ![]() ,
,
则PM=3﹣ ![]() t.
t.
根据直线和圆相切,则圆心到直线的距离等于圆的半径,得
3﹣ ![]() t =1,t=
t =1,t= ![]() .
.
此时⊙P与直线CD显然相离;
②当⊙P和OC第二次相切时,
则有 ![]() t﹣3=1,t=
t﹣3=1,t= ![]() .
.
此时⊙P与直线CD显然相交;
答:当t= ![]() 或
或 ![]() 时⊙P和OC相切,t=
时⊙P和OC相切,t= ![]() 时⊙P和直线CD相离,当t=
时⊙P和直线CD相离,当t= ![]() 时⊙P和直线CD相交.
时⊙P和直线CD相交.
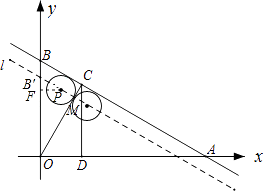
【解析】(1)过点P向y轴引垂线.根据已知点A、B的坐标可以求得∠BAO=30°,从而可以结合题意,利用解直角三角形的知识进行求解;(2)此题应分作两种情况考虑:①当P位于OC左侧,⊙P与OC第一次相切时,易证得∠COB=∠BAO=30°,设直线l与OC的交点为M,根据∠BOC的度数,即可求得B′M、PM的表达式,而此时⊙P与OC相切,可得PM=1,由此可列出关于t的方程,求得t的值,进而可判断出⊙P与CD的位置关系;②当P位于OC右侧,⊙P与OC第二次相切时,方法与①相同.


科目:初中数学 来源: 题型:
【题目】如图1,△ABC的边BC在直线l上,AC⊥BC,且AC=BC,△EFP的边FP也在直线l上,边EF与边AC重合,且EF=FP.
(1)直接写出AB与AP所满足的数量关系:_____,AB与AP的位置关系:_____;
(2)将△ABC沿直线l向右平移到图2的位置时,EP交AC于点Q,连接AP,BQ,求证:AP=BQ;
(3)将△ABC沿直线l向右平移到图3的位置时,EP的延长线交AC的延长线于点Q,连接AP,BQ,试探究AP=BQ是否仍成立?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有许多代数恒等式可以用图形的面积来表示,如图![]() ,它表示了
,它表示了![]()
![]() 图
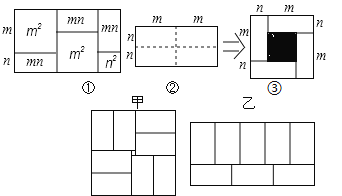
图![]() 是将一个长2m、宽2n的长方形,沿图中虚线平方为四块小长方形,然后再拼成一个正方形
是将一个长2m、宽2n的长方形,沿图中虚线平方为四块小长方形,然后再拼成一个正方形![]() 图
图![]() ,则图
,则图![]() 中的阴影部分的正方形的边长等于______
中的阴影部分的正方形的边长等于______![]() 用含m、n的代数式表示
用含m、n的代数式表示![]()
![]() 请用两种不同的方法列代数式表示图
请用两种不同的方法列代数式表示图![]() 中阴影部分的面积.
中阴影部分的面积.
方法![]() ______方法
______方法![]() ______
______
![]() 请你观察图形
请你观察图形![]() ,写出三个代数式
,写出三个代数式![]() 、
、![]() 、mn关系的等式:______;
、mn关系的等式:______;
![]() 根据
根据![]() 题中的等量关系,解决如下问题:若已知
题中的等量关系,解决如下问题:若已知![]() ,
,![]() ,则
,则![]() ______;
______;
![]() 小明用8个一样大的长方形
小明用8个一样大的长方形![]() 长acm,宽
长acm,宽![]() 拼图,拼出了如图甲、乙的两种图案,图案甲是一个正方形,图案乙是一个大的长方形,图案甲的中间留下了边长是2cm的正方形小洞
拼图,拼出了如图甲、乙的两种图案,图案甲是一个正方形,图案乙是一个大的长方形,图案甲的中间留下了边长是2cm的正方形小洞![]() 则
则![]() 的值为______.
的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市某幼儿园六一期间举行亲子游戏,主持人请三位家长分别带自己的孩子参加游戏,主持人准备把家长和孩子重新组合完成游戏,A、B、C分别表示三位家长,他们的孩子分别对应的是a、b、c.
(1)若主持人分别从三位家长和三位孩子中各选一人参加游戏,恰好是A、a的概率是多少(直接写出答案)
(2)若主持人先从三位家长中任选两人为一组,再从孩子中任选两人为一组,四人共同参加游戏,恰好是两对家庭成员的概率是多少.(画出树状图或列表)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把△ABC纸片沿DE折叠,当点A落在四边形BCED的外部时,则∠A与∠1和∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是( )

A. 2∠A=∠1﹣∠2 B. 3∠A=2(∠1﹣∠2)
C. 3∠A=2∠1﹣∠2 D. ∠A=∠1﹣∠2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,BE平分
,BE平分![]() ,
,![]() .
.
![]() 与BC平行吗?请说明理由;
与BC平行吗?请说明理由;
![]() 与EF的位置关系如何?为什么?
与EF的位置关系如何?为什么?
解:![]() 理由如下:
理由如下:
![]() 平角的定义
平角的定义![]()
![]() 已知
已知![]()
![]() ______
______![]() ______
______![]()
![]() ______
______
![]() 与EF的位置关系是______
与EF的位置关系是______
![]() 平分
平分![]() 已知
已知![]()
![]() 角平分线的定义
角平分线的定义![]()
又![]() ,
,![]() 已知
已知![]() 即
即![]()
![]() ______
______![]() 等量代换
等量代换![]()
![]() ______
______![]() ______
______![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平行四边形ABCD中,∠ABE=∠AEB,AE∥DF,DC是∠ADF的角平分线.下列说法正确的是( )
①BE=CF ②AE是∠DAB的角平分线 ③∠DAE+∠DCF=120°.

A. ① B. ①② C. ①②③ D. 都不正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙P的圆心为P(﹣3,2),半径为3,直线MN过点M(5,0)且平行于y轴,点N在点M的上方. 
(1)在图中作出⊙P关于y轴对称的⊙P′.根据作图直接写出⊙P′与直线MN的位置关系.
(2)若点N在(1)中的⊙P′上,求PN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,D、E分别为AC、AB的中点,连DE、CE.则下列结论中不一定正确的是( ) 
A.ED∥BC
B.ED⊥AC
C.∠ACE=∠BCE
D.AE=CE
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com