【题目】如图，AD是半圆的直径，点C是弧BD的中点，∠BAD=70°，则∠ADC等于（ ）
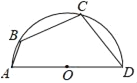
A. 50° B. 55° C. 65° D. 70°
举一反三期末百分冲刺卷系列答案科目：初中数学 来源： 题型：
【题目】如图某小船准备从
处出发，沿北偏东
的方向航行，在规定的时间将一批物资运往
处的货船上，后考虑这条航线可能会因退潮而使小船搁浅，决定改变航线，从处出发沿正东方向航行
海里到达
处，再由处沿北偏东
的方向航行到达处．
（1）小船由经到达走了多少海里（结果精确到
海里）；
（2）为了按原定时间到达处的货船上，小船提速，每小时增加
海里，求小船原定的速度（结果精确到
海里/时）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知二次函数y=ax2+bx+c（a≠0）的图象如图所示有下列4个结论：①abc＞0；②b＜a+c；③4a+2b+c＞0；④a+b＞m（am+b）（m≠1的实数），其中正确结论的个数为（ ）
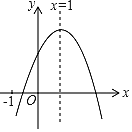
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，等腰三角形ABC中，AB＝AC＝4，∠BAC＝100°，点D是底边BC的动点（点D不与B、C重合），连接AD，作∠ADE＝40°，DE与AC交于点E．
（1）当DC等于多少时，△ABD与△DCE全等？请说明理由；
（2）在点D的运动过程中，△ADE的形状可以是等腰三角形吗？若可以，求出∠BDA的度数；若不可以，请说明理由．
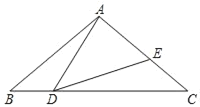
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下表是二次函数
的部分
的对应值：
x | … | －1 |
| 0 |
| 1 |
| 2 |
| 3 | … |
y | … | m |
| －1 |
| －2 |
| －1 |
| 2 | … |
(1)求函数解析式；
(2)当
时，y的取值范围是___________；
(3)当抛物线的顶点在直线
的下方时，n的取值范围是__________.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABD和△ACE中，有下列四个等式：①AB=AC；②AD=AE；③∠1=∠2；④BD=CE．以其中三个条件为题设，填入已知栏中，一个论断为结论，填入下面求证栏中，使之组成一个真命题，并写出证明过程．
已知： ．
求证： ．
证明：
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图，等边△ABC的边长为8，D为AC上的一个动点，延长AB到点E，使BE=CD，连接DE交BC于点P
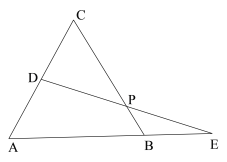
（1）求证：DP=EP；
（2）若D为AC的中点，求BP的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】类比转化、从特殊到一般等思想方法，在数学学习和研究中经常用到，如下是一个案例，请补充完整.
（1）尝试探究
如图（1），在正方形ABCD中，对角线AC、BD相交于点O，点E是BC边上一点，AE与BD交于点G，过点E作EF⊥AE交AC于点F，若
=2，则
的值是 ；
（2）拓展迁移
如图（2），在矩形ABCD中，过点B作BH⊥AC于点O，交AD相于点H，点E是BC边上一点，AE与BH相交于点G，过点E作EF⊥AE交AC于点F.
①若∠BAE=∠ACB，sin∠EAF=
，求tan∠ACB；
②若
，
=b（a＞0，b＞0），求的值（用含a，b的代数式表示）．
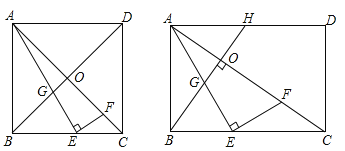
图（1） 图（2）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
