练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

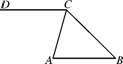
    如图4­1­21，已知∠ACD＝70°，∠ACB＝60°，∠ABC＝50°.求证：AB∥CD.


    证明：∵∠ACD＝70°，∠ACB＝60°，∴∠BCD＝130°.

    ∵∠ABC＝50°，∴∠BCD＋∠ABC＝180°.

    ∴AB∥CD.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


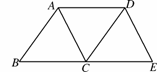
    如图4­3­36，将△ABC沿BC方向平移得到△DCE，连接AD，下列条件中能够判定四边形ACED为菱形的是(　　)

    A．AB＝BC  B．AC＝BC  C．∠B＝60°  D．∠ACB＝60°

            

    查看答案和解析>>

    科目：初中数学 来源： 题型：


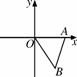
    如图6­4­19，在平面直角坐标系xOy中，点A，B的坐标分别为(3,0)，(2，－3)，△AB′O′是△ABO关于点A的位似图形，且O′的坐标为(－1,0)，则点B′的坐标为________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


     (1)观察发现．

    如图6­1­24(1)：若点A，B在直线m的同侧，在直线m上找一点P，使AP＋BP的值最小，做法如下：作点B关于直线m的对称点B′，连接AB′，与直线m的交点就是所求的点P，线段AB′的长度即为AP＋BP的最小值．

    如图6­1­24(2)：在等边三角形ABC中，AB＝2，点E是AB的中点，AD是高，在AD上找一点P，使BP＋PE的值最小，做法如下：作点B关于AD的对称点，恰好与点C重合，连接CE交AD于一点．则这就是所求的点P，故BP＋PE的最小值为__________________．

    　　　　　　　　　

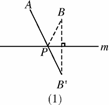
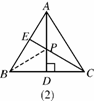
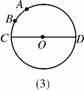
    图6­1­24

    (2)实践运用．

    如图6­1­24(3)：已知⊙O的直径CD为2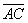，的度数为60°，点B是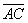的中点，在直径CD上作出点P，使BP＋AP的值最小，则BP＋AP的最小值为________________．

    (3)拓展延伸．

    如图6­1­24(4)：点P是四边形ABCD内一点，分别在边AB，BC上作出点M，N，使PM＋PN的值最小，保留作图痕迹，不写作法．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    下列命题中，属于真命题的是(　　)

    A．相等的角是直角  B．不相交的两条线段平行

    C．两直线平行，同位角互补  D．经过两点有且只有一条直线

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知二元一次方程3x－y=1，当x=2时，y等于（      ）

         A．5         B．－3         C．－7          D．7

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    2014年某市有28000名初中毕业生参加了升学考试,为了了解28000 名考生的升学成绩,从中抽取了300名考生的试卷进行统计分析,以下说法正确的是(      )

      A．28000名考生是总体                B.每名考生的成绩是个体

    C.300名考生是总体的一个样本         D.以上说法都不正确

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知，如图，CD⊥AB于D，EF⊥AB于F，∠1=∠2，请问DG∥BC吗？如果平行，请说明理由。

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，点D是△ABC的边BC上任意一点，点E、F分别是线段AD、CE的中点，则△ABC的面积等于△BEF的面积的                               （    ）

    A.2倍             B.3倍                  C.4倍                D.5倍

     


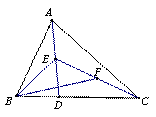    查看答案和解析>>

    同步练习册答案