
分析 根据二次根式的乘法法则、除法法则、二次根式的性质化简即可.
解答 解:(1)$\sqrt{\frac{64}{9}×\frac{144}{169}}$=$\sqrt{\frac{64}{9}}$×$\sqrt{\frac{144}{169}}$=$\frac{8}{3}$×$\frac{12}{13}$=$\frac{32}{13}$;
(2)$\sqrt{(-5)^{2}×(-3)^{2}}$=$\sqrt{{5}^{2}×{3}^{2}}$=$\sqrt{{5}^{2}}$×$\sqrt{{3}^{2}}$=5×3=15;
(3)$\sqrt{8{a}^{2}{b}^{3}}$=$\sqrt{4{a}^{2}{b}^{2}×2b}$=2ab$\sqrt{2b}$;
(4)∵a>0,b≥0,
∴$\sqrt{\frac{{b}^{3}}{8{a}^{2}}}$=$\frac{\sqrt{{b}^{3}}}{\sqrt{8{a}^{2}}}$=$\frac{b\sqrt{b}}{2\sqrt{2}a}$=$\frac{b\sqrt{2b}}{4a}$.
点评 本题考查的是二次根式的化简,掌握二次根式的性质:$\sqrt{{a}^{2}}$=|a|是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
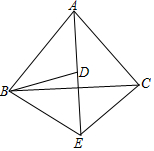 如图所示,已知$\frac{AB}{BD}$=$\frac{BC}{BE}$=$\frac{CA}{ED}$.∠ABD=20°,求∠EBC的大小.
如图所示,已知$\frac{AB}{BD}$=$\frac{BC}{BE}$=$\frac{CA}{ED}$.∠ABD=20°,求∠EBC的大小.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x+4=0}\\{\frac{1}{x}-5>0}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{{x}^{2}-x=0}\\{x+1<0}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{y+2>0}\\{x-y<0}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{2x-5>0}\\{x<0}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com