
分析 根据题意即可求出答案.
解答 解:方法一:原式=$\frac{2(\sqrt{5}-\sqrt{3})}{(\sqrt{5}+\sqrt{3})(\sqrt{5}-\sqrt{3})}$=$\frac{2(\sqrt{5}-\sqrt{3})}{5-3}$=$\sqrt{5}-\sqrt{3}$
方法二:原式=$\frac{5-3}{\sqrt{5}+\sqrt{3}}$=$\frac{(\sqrt{5})^{2}-(\sqrt{3})^{2}}{\sqrt{5}+\sqrt{3}}$=$\frac{(\sqrt{5}+\sqrt{3})(\sqrt{5}-\sqrt{3})}{\sqrt{5}+\sqrt{3}}$=$\sqrt{5}-\sqrt{3}$
点评 本题考查分母有理化,解题的关键是熟练运用平方差公式,本题属于基础题型.


 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:解答题
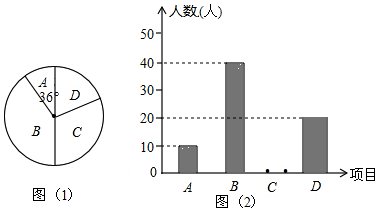
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
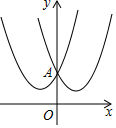 如果两个二次函数的图象关于y轴对称,我们就称这两个二次函数互为“关于y轴对称二次函数”,如图所示二次函数y1=x2+2x+2与y2=x2-2x+2是“关于y轴对称二次函数”.
如果两个二次函数的图象关于y轴对称,我们就称这两个二次函数互为“关于y轴对称二次函数”,如图所示二次函数y1=x2+2x+2与y2=x2-2x+2是“关于y轴对称二次函数”.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{9}$-$\sqrt{4}$=$\sqrt{5}$ | B. | |1-$\sqrt{3}$|=$\sqrt{3}$-1 | C. | $\sqrt{9}$=±3 | D. | -$\sqrt{(-9)^{2}}$=9 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
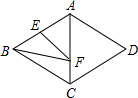 如图,菱形ABCD的边长为4,∠BAD=120°,点E是AB的中点,点F是AC上的一动点,则EF+BF的最小值是( )
如图,菱形ABCD的边长为4,∠BAD=120°,点E是AB的中点,点F是AC上的一动点,则EF+BF的最小值是( )| A. | 4 | B. | 2$\sqrt{3}$ | C. | 4$\sqrt{3}$ | D. | 2$\sqrt{7}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com