
如图,在Rt△ABC中,∠ACB=90º,∠B=30º,将△ABC绕点C按顺时针方向旋转n度后,得到△DEC,点D刚好落在AB边上.
(1)求n的值;
(2)若F是DE的中点,判断四边形ACFD
的形状,并说明理由.
 |
科目:初中数学 来源: 题型:
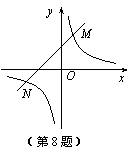
如图,双曲线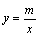 与直线
与直线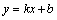 相交于点M,N,且点M的坐标为(1,3),点N的纵坐标为
相交于点M,N,且点M的坐标为(1,3),点N的纵坐标为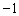 .根据图象信息可得关于x的方程
.根据图象信息可得关于x的方程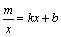 的解为( )
的解为( )
A.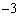 ,1 B.
,1 B.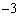 ,3 C.
,3 C.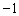 ,1 D.
,1 D.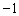 ,3
,3
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
科学家为了推测最适合某种珍奇植物生长的温度,将这种植物分别放在不同温度的环境中,经过一定时间后,测试出这种植物高度的增长
 情况,部分数据如下表:
情况,部分数据如下表:
| 温度t/℃ | -4 | -2 | 0 | 1 | 4 |
| 植物高度增长量l/mm | 41 | 49 | 49 | 46 | 25 |
科学家经过猜想、推测出l与t之间是二次函数关系.由
此可以推测最适合这种植物生长的温度为 ℃.
查看答案和解析>>
科目:初中数学 来源: 题型:
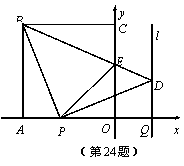
如图,正方形OABC的边OA,OC在坐标轴上,点B的坐标为(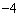 ,4).点P从点A出发,以每秒1个单位长度的速度沿x轴向点O运动;点Q从点O同时出发,以相同的速度沿x轴的正方向运动,规定点P到达点O时,点Q也停止运动.连接BP,过P点作BP的垂线,与过点Q平行于y轴的直线l相交于点D.BD与
,4).点P从点A出发,以每秒1个单位长度的速度沿x轴向点O运动;点Q从点O同时出发,以相同的速度沿x轴的正方向运动,规定点P到达点O时,点Q也停止运动.连接BP,过P点作BP的垂线,与过点Q平行于y轴的直线l相交于点D.BD与 轴交于点E,连接PE.设点P运动的时间为t(s).
轴交于点E,连接PE.设点P运动的时间为t(s).
(1)∠PBD的度数为 ,
点D的坐标为 (用t表示);
(2)当t为何值时,△PBE 为等腰三角形?
(3)探索△POE周长是否随时间t的变化而变化,若变化,说明理由;若不变,试求这个定值.
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com