
【题目】如图,将平行四边形ABCD的边DC延长至点E,使CE=DC,连接AE,交BC于点F.
(1)求证:△ABF≌△ECF;
(2)连接AC、BE,则当∠AFC与∠D满足什么条件时,四边形ABEC是矩形?请说明理由.

【答案】(1)证明见解析;(2)当∠AFC=2∠D时,四边形ABEC是矩形.理由见解析.
【解析】
试题(1)由四边形ABCD是平行四边形,CE=DC,易证得∠ABF=∠ECF,∠AFB=∠EFC,AB=EC,则可证得△ABF≌△ECF;
(2)首先根据四边形ABCD是平行四边形,得到四边形ABEC是平行四边形,然后证得FC=FE,利用对角线互相相等的四边形是矩形判定四边形ABEC是矩形.
试题解析:(1)证明:在平行四边形ABCD中,AB∥CD,AB=CD,
∴∠BAE=∠AEC,
又∵CE=CD,
∴AB=CE,
在△ABF和△ECF中,
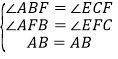 ,
,
∴△ABF≌△ECF(AAS);
(2)当∠AFC=2∠D时,四边形ABEC是矩形.
∵四边形ABCD是平行四边形,
∴BC∥AD,∠BCE=∠D,
由题意易得AB∥EC,AB∥EC,
∴四边形ABEC是平行四边形.
∵∠AFC=∠FEC+∠BCE,
∴当∠AFC=2∠D时,则有∠FEC=∠FCE,
∴FC=FE,
∴四边形ABEC是矩形.


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=24,D是BC的中点,AC的垂直平分线EF分别交AC、AD于点E、F,EF = 5 .

(1)求点F到边AB的距离FG的长;
(2)求 F到B点的距离FB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠ABC=90°,AB=BC.直线l与以BC为直径的圆O相切于点C.点F是圆O上异于B、C的动点,直线BF与l相交于点E,过点F作AF的垂线交直线BC与点D.
(1)如果BE=15,CE=9,求EF的长;
(2)证明:①△CDF∽△BAF;②CD=CE;
(3)探求动点F在什么位置时,相应的点D位于线段BC的延长线上,且使BC=![]() CD,请说明你的理由.
CD,请说明你的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰Rt△ABC中,∠C=90°,D是斜边上AB上任一点,AE⊥CD于E,BF⊥CD交CD的延长线于F,CH⊥AB于H点,交AE于G.
(1)试说明AH=BH
(2)求证:BD=CG.
(3)探索AE与EF、BF之间的数量关系

查看答案和解析>>
科目:初中数学 来源: 题型:
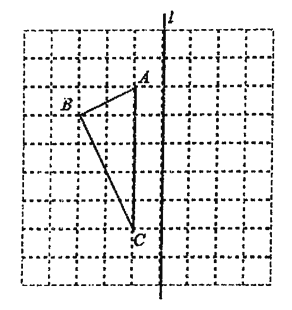
【题目】如图,正方形网格中每个小正方形边长都是1.
(1)画出△ABC关于直线1对称的图形△A1BlCl;
(2)在直线l上找一点P,使PB=PC;(要求在直线1上标出点P的位置)
(3)连接PA、PC,计算四边形PABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AO平分∠BAC,AO⊥BC,DE⊥BC,GH⊥BC,垂足分别为O、E、H,且DO∥AC,∠B=43°,则图中角的度数为47°的角的个数是( )

A. 5 B. 6 C. 7 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,M、N是对角线AC上的两个动点,P是正方形四边上的任意一点,且AB=4,MN=2,设AM=x,在下列关于△PMN是等腰三角形和对应P点个数的说法中,
①当x=0(即M、A两点重合)时,P点有6个;
②当P点有8个时,x=2![]() ﹣2;
﹣2;
③当△PMN是等边三角形时,P点有4个;
④当0<x<4![]() ﹣2时,P点最多有9个.
﹣2时,P点最多有9个.
其中结论正确的是( )

A. ①② B. ①③ C. ②③ D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小组做“用频率估计概率”的实验时,绘出的某一结果出现的频率折线图,则符合这一结果的实验可能是( )

A. 抛一枚硬币,出现正面朝上
B. 掷一个正六面体的骰子,出现3点朝上
C. 一副去掉大小王的扑克牌洗匀后,从中任抽一张牌的花色是红桃
D. 从一个装有2个红球1个黑球的袋子中任取一球,取到的是黑球
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com