
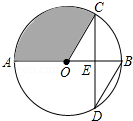
 如图,AB是⊙O的直径,弦CD交AB于点E,且E为OB的中点,∠CDB=30°,CD=4$\sqrt{3}$,则阴影部分的面积$\frac{16}{3}$π.
如图,AB是⊙O的直径,弦CD交AB于点E,且E为OB的中点,∠CDB=30°,CD=4$\sqrt{3}$,则阴影部分的面积$\frac{16}{3}$π. 分析 根据圆周角定理求出∠COB,求出∠AOC,根据垂径定理求出∠OEC=90°,CE=2$\sqrt{3}$,解直角三角形求出OC,根据扇形面积公式求出即可.
解答 解:∵∠CDB=30°,
∴∠COB=2∠CDB=60°,
∴∠AOC=120°,
∵E为OB的中点,OB过O,CD=4$\sqrt{3}$,
∴CE=DE=2$\sqrt{3}$,∠OEC=90°,
∴OC=$\frac{CE}{sin60°}$=4,
∴阴影部分的面积为$\frac{120π×{4}^{2}}{360}$=$\frac{16}{3}$π,
故答案为:$\frac{16}{3}$π;
点评 本题考查了圆周角定理,垂径定理,解直角三角形,扇形面积公式等知识点,能求出线段OC的长和∠AOC的度数是解此题的关键.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:填空题
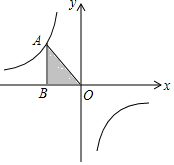 如图,已知反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象经过点A,过A点作AB⊥x轴,垂足为B.若△AOB的面积为1,则k=-2.
如图,已知反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象经过点A,过A点作AB⊥x轴,垂足为B.若△AOB的面积为1,则k=-2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一垂直于水平地面的灯柱AB被一钢筋CD固定,CD与地面成45°角(∠CDB=45°),在点C上方2m处加固另一条钢筋DE,DE与地面成60°角(∠EDB=60°),则钢筋DE的长度约为多少?(结果精确到0.1m,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
如图,一垂直于水平地面的灯柱AB被一钢筋CD固定,CD与地面成45°角(∠CDB=45°),在点C上方2m处加固另一条钢筋DE,DE与地面成60°角(∠EDB=60°),则钢筋DE的长度约为多少?(结果精确到0.1m,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
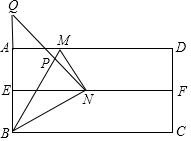 如图,四边形ABCD为矩形纸片,对折纸片,使得AD与BC重合,得到折痕EF,把纸片展平后,再把纸片沿着BM折叠,使得点A与EF上的点N重合,在折痕BM上取一点P,使得BP=BA,连接NP并延长.交BA的延长线于点Q.若AB=6.则AQ的长为3$\sqrt{3}$-3.
如图,四边形ABCD为矩形纸片,对折纸片,使得AD与BC重合,得到折痕EF,把纸片展平后,再把纸片沿着BM折叠,使得点A与EF上的点N重合,在折痕BM上取一点P,使得BP=BA,连接NP并延长.交BA的延长线于点Q.若AB=6.则AQ的长为3$\sqrt{3}$-3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com