
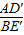 的值为1,求∠AFB的度数;
的值为1,求∠AFB的度数; ,BC=
,BC= ,①求
,①求 的值和∠AFB的度数;②若E为BC的中点,求△OBC面积的最大值.
的值和∠AFB的度数;②若E为BC的中点,求△OBC面积的最大值.
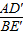 的值,可以通过证明△CBE′≌△CAD′,得到AD′=BE′求出,求∠AFB的度数,通过△AOF与△BOC比较得出;
的值,可以通过证明△CBE′≌△CAD′,得到AD′=BE′求出,求∠AFB的度数,通过△AOF与△BOC比较得出;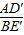 的值和∠AFB的度数,可以通过证明△CBE′∽△CAD′得到;要求△OBC面积的最大值,因为∠ACB=60°,BC=
的值和∠AFB的度数,可以通过证明△CBE′∽△CAD′得到;要求△OBC面积的最大值,因为∠ACB=60°,BC=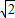 ,即求CO的最大值,用面积公式结合三角函数可以得出.
,即求CO的最大值,用面积公式结合三角函数可以得出.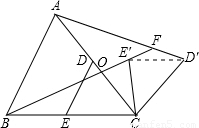
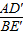 的值为1,
的值为1,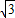 ,BC=
,BC=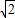 ,DE∥AB,
,DE∥AB,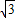 :
: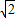 ,CD:CE=
,CD:CE=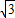 :
: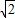 =CD′:CE′,
=CD′:CE′,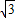 :
: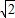 ,
,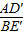 =
=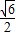 ,∠CBF=∠CAD′,
,∠CBF=∠CAD′,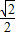 ,△OBC面积的最大值=0.5BC•sin∠ACB•CO=
,△OBC面积的最大值=0.5BC•sin∠ACB•CO=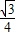 .
.

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:2009年湖北省黄石市十六中中考数学模拟试卷(解析版) 题型:选择题

查看答案和解析>>
科目:初中数学 来源:2007年江苏省徐州市中考数学试卷(解析版) 题型:解答题
 的值为1,求∠AFB的度数;
的值为1,求∠AFB的度数; ,BC=
,BC=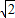 ,①求
,①求 的值和∠AFB的度数;②若E为BC的中点,求△OBC面积的最大值.
的值和∠AFB的度数;②若E为BC的中点,求△OBC面积的最大值.
查看答案和解析>>
科目:初中数学 来源:2007年江苏省徐州市中考数学试卷(解析版) 题型:解答题
 ≈1.41,
≈1.41, ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源:2007年江苏省徐州市中考数学试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com