Question

已知：等边的边长为．

探究（1）：如图１，过等边的顶点依次作的垂线围成求证：是等边三角形且；

探究（2）：在等边内取一点，过点分别作垂足分别为点

①如图2，若点是的重心，我们可利用三角形面积公式及等边三角形性质得到两个正确结论（不必证明）：结论1．；结论2．；

②如图3，若点是等边内任意一点，则上述结论是否仍然成立？如果成立，请给予证明；如果不成立，请说明理由．

 

Answer 1

证明：如图1，为等边三角形

∴

同理：

为等边三角形．

在中，

在中，

（2）：结论1成立.

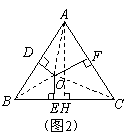证明；方法一：如图2，连接

由=

作垂足为，

则

方法二：如图3，过点作分别交于点，过点

作于点，

是等边三角形

四边形是矩形

在中，

在中，

在中，

                               

（2）结论2成立．

证明：方法一：如图４，过顶点依次作边的垂线围成由（1）得为等边三角形且················ 9分

过点分别作于,于于点于点

由结论1得：

又

四边形为矩形

同理：，

方法二：（同结论1方法二的辅助线）

在中，

在中，

同理：

=

=

由结论1得：

方法三：如图5，连接，根据勾股定理得：

：

整理得：

分