
分析 (1)两式相加即可求得答案.
(2)先求出x2+2x的值,然后整体代入进行计算即可得解.
(3)由x2-x-1=0,得到x2=x+1,-x2+x=-1;将所给的代数式变形、化简、求值,即可解决问题.
解答 解:(1)∵mn-n=15,m-mn=6,
∴两式相加得到:m-n=21;
(2)∵x2+2x-5=3,
∴x2+2x=8,
∴2x2+4x+8=2(x2+2x)+8=24;
(3)∵x2-x-1=0,
∴x2=x+1,-x2+x=-1,
∴-x3+2x+2015
=-x(x+1)+2x+2015
=-x2-x+2x+2015
=-x2+x+2015
=2014.
点评 该题主要考查了因式分解在代数式的化简、求值等方面的应用问题;解题的关键是运用因式分解法,灵活将所给的条件、所要化简的代数式变形、化简、运算、求值.


 新思维寒假作业系列答案
新思维寒假作业系列答案科目:初中数学 来源: 题型:选择题
| A. | a=3,b=6,c=2,d=4 | B. | a=1,b=$\sqrt{2}$,c=2$\sqrt{2}$,d=4 | ||
| C. | a=4,b=5,c=8,d=10 | D. | a=2,b=3,c=4,d=5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
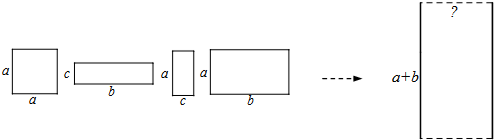
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
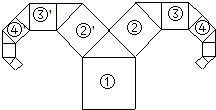 如图所示为一种“羊头”形图案,其作法是从正方形①开始,以它的一边为斜边,向外作等腰直角三角形,然后再以其直角边为边,分别向外作正方形②和②',…,依此类推,若正方形①的面积为64,则正方形④的面积为8.
如图所示为一种“羊头”形图案,其作法是从正方形①开始,以它的一边为斜边,向外作等腰直角三角形,然后再以其直角边为边,分别向外作正方形②和②',…,依此类推,若正方形①的面积为64,则正方形④的面积为8.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
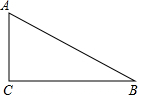 用直尺、圆规作图,不写作法,但要保留作图痕迹.
用直尺、圆规作图,不写作法,但要保留作图痕迹.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 入住的房间数量 | 房间价格 | 总维护费用 | |
| 提价前 | 60 | 200 | 60×20 |
| 提价后 | 60-$\frac{x}{10}$ | 200+x | (60-$\frac{x}{10}$)×20 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
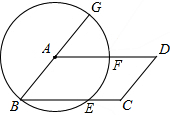 如图,以?ABCD的顶点A为圆心,AB为半径作⊙A,分别交BC,AD于E,F两点,交BA的延长线于G,判断弧$\widehat{EF}$和弧$\widehat{FG}$是否相等,并说明理由.
如图,以?ABCD的顶点A为圆心,AB为半径作⊙A,分别交BC,AD于E,F两点,交BA的延长线于G,判断弧$\widehat{EF}$和弧$\widehat{FG}$是否相等,并说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com