
【题目】如图,在矩形ABCO中,AO=3,tan∠ACB=![]() ,以O为坐标原点,OC为
,以O为坐标原点,OC为![]() 轴,OA为
轴,OA为![]() 轴建立平面直角坐标系。设D,E分别是线段AC,OC上的动点,它们同时出发,点D以每秒3个单位的速度从点A向点C运动,点E以每秒1个单位的速度从点C向点O运动,设运动时间为
轴建立平面直角坐标系。设D,E分别是线段AC,OC上的动点,它们同时出发,点D以每秒3个单位的速度从点A向点C运动,点E以每秒1个单位的速度从点C向点O运动,设运动时间为![]() 秒。
秒。
(1)求直线AC的解析式;
(2)用含![]() 的代数式表示点D的坐标;
的代数式表示点D的坐标;
(3)当![]() 为何值时,△ODE为直角三角形?
为何值时,△ODE为直角三角形?
(4)在什么条件下,以Rt△ODE的三个顶点能确定一条对称轴平行于![]() 轴的抛物线?并请选择一种情况,求出所确定抛物线的解析式.
轴的抛物线?并请选择一种情况,求出所确定抛物线的解析式.

【答案】(1)![]() ;(2)D(
;(2)D(![]() ,
,![]() );(3)
);(3)![]() ,
,![]() ,
,![]() ,
,![]() ;(4)
;(4)![]()
【解析】
(1)在Rt△AOC中,已知AO的长以及∠ACB的正弦值,能求出OC的长,即可确定点C的坐标,利用待定系数法能求出直线AC的解析式.
(2)过D作AO、OC的垂线,通过构建相似三角形来求出点D的坐标.
(3)用t表示出OD、DE、OE的长,若△ODE为直角三角形,那么三边符合勾股定理,据此列方程求出对应的t的值.
(4)根据(3)的结论能得到t的值,△ODE中,当OD⊥x轴或DE垂直x轴时,都不能确定“一条对称轴平行于y轴的抛物线”,余下的情况都是符合要求的,首先得D、E的坐标,再利用待定系数法求出抛物线的解析式.
(1)根据题意,得CO=AB=BCtan∠ACB=4,则A(0,3)、B(4,3)、C(4,0);
设直线AC的解析式为:y=kx+3,代入C点坐标,得:
4k+3=0,k=-![]() ,
,
∴直线AC:![]() ;
;
(2)分别作DF⊥AO,DH⊥CO,垂足分别为F,H,
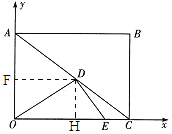
则有△ADF∽△DCH∽△ACO,
∴AD:DC:AC=AF:DH:AO=FD:HC:OC,
而AD=![]() (其中0≤
(其中0≤![]() ≤
≤![]() ),OC=AB=4,AC=5,∴FD=
),OC=AB=4,AC=5,∴FD=![]() AD=
AD=![]() ,AF=
,AF=![]() AD=
AD=![]() ,
,
DH=![]() ,HC=
,HC=![]() ,
,
∴D(![]() ,
,![]() );
);
(3)CE=![]() ,E(
,E(![]() ,0),OE=OC-CE=4-
,0),OE=OC-CE=4-![]() ,HE=|CH-CE|=
,HE=|CH-CE|=![]() ,
,
则OD2=DH2+OH2=![]() =
=![]() ,
,
DE2=DH2+HE2=![]() =
=![]() ,
,
当△ODE为Rt△时,有OD2+DE2=OE2,或OD2+OE2=DE2,或DE2+OE2=OD2,
即![]() ①,
①,
或![]() ②,
②,
或![]() ③,
③,
上述三个方程在0≤![]() ≤
≤![]() 内的所有实数解为
内的所有实数解为
![]() ,
,![]() ,
,![]() ,
,![]() ;
;
(4)当DO⊥OE,及DE⊥OE时,即![]() 和
和![]() 时,以Rt△ODE的三个顶点不确定对称轴平行于
时,以Rt△ODE的三个顶点不确定对称轴平行于![]() 轴的抛物线,其它两种情况都可以各确定一条对称轴平行于
轴的抛物线,其它两种情况都可以各确定一条对称轴平行于![]() 轴的抛物线D(
轴的抛物线D(![]() ,
,![]() ),E(4-
),E(4-![]() ,0),
,0),
当![]() 时,D(
时,D(![]() ,
,![]() ),E(3,0),因为抛物线过O(0,0),
),E(3,0),因为抛物线过O(0,0),
所以设所求抛物线为![]() ,将点D,E坐标代入,求得
,将点D,E坐标代入,求得![]() ,
,![]() ,
,
∴所求抛物线为![]() .
.
(当![]() 时,所求抛物线为
时,所求抛物线为![]() ).
).


科目:初中数学 来源: 题型:
【题目】我们知道,任意一个正整数n都可以进行这样的分解:n=p×q(p,q是正整数,且p≤q),在n的所有这种分解中,如果p,q两因数之差的绝对值最小,我们就称p×q是n的最佳分解.并规定:F(n)=![]() .例如12可以分解成1×12,2×6或3×4,因为12﹣1>6﹣2>4﹣3,所以3×4是12的最佳分解,所以F(12)=
.例如12可以分解成1×12,2×6或3×4,因为12﹣1>6﹣2>4﹣3,所以3×4是12的最佳分解,所以F(12)= ![]() .
.
(1)若F(a)=![]() 且a为100以内的正整数,则a=________;
且a为100以内的正整数,则a=________;
(2)如果m是一个两位数,那么试问F(m)是否存在最大值或最小值?若存在,求出最大(或最小)值以及此时m的取值并简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了增强学生体质,决定开设以下体育课外活动项目:A:篮球 B:乒乓球C:羽毛球 D:足球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:


(1)这次被调查的学生共有 人;
(2)请你将条形统计图(2)补充完整;
(3)在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠2,AC=AD,要使△ABC≌△AED,还需添加一个条件,那么在①AB=AE,②BC=ED,③∠C=∠D,④∠B=∠E,这四个关系中可以选择的是( )
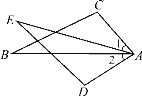
A. ①②③ B. ①②④ C. ①③④ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的材料
勾股定理神秘而美妙,它的证法多种多样,下面是教材中介绍的一种拼图证明勾股定理的方法.

先做四个全等的直角三角形,设它们的两条直角边分别为a,b,斜边为c,然后按图1的方法将它们摆成正方形.
由图1可以得到![]() ,
,
整理,得![]() .
.
所以![]() .
.
如果把图1中的四个全等的直角三角形摆成图2所示的正方形,
请你参照上述证明勾股定理的方法,完成下面的填空:
由图2可以得到 ,
整理,得 ,
所以 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A是半径为12cm的⊙O上的定点,动点P从A出发,以2πcm/s的速度沿圆周逆时针运动,当点P回到点A立即停止运动.
(1)如果∠POA=90°,求点P运动的时间;
(2)如果点B是OA延长线上的一点,AB=OA,那么当点P运动的时间为2s时,判断直线BP与⊙O的位置关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长是4,点E是AB边上一动点,连接CE,过点B作BG⊥CE于点G,点P是AB边上另一动点,则PD+PG的最小值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图所示,正方形![]() 的边长为1,
的边长为1,![]() 为
为![]() 边上的一个动点(点
边上的一个动点(点![]() 与
与![]() 、
、![]() 不重合),以
不重合),以![]() 为一边向正方形
为一边向正方形![]() 外作正方形
外作正方形![]() ,连接
,连接![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.

(1)求证:①![]() ≌△
≌△![]() . ②
. ②![]() .
.
(2)当![]() 平分
平分![]() 时,求
时,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,PM、QN分别垂直平分AB、AC,交BC于点P、Q, P点在Q点左侧.
(1)BC=10,求△APQ的周长;
(2)若∠BAC=![]() ,∠PAQ=
,∠PAQ=![]() ,求
,求![]() 与
与![]() 的关系,并指出
的关系,并指出![]() 的取值范围.
的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com