
【题目】如图,在![]() 中,
中,![]() ,AD、BD、CD分别平分
,AD、BD、CD分别平分![]() 的外角
的外角![]() ,内角
,内角![]() ,外角
,外角![]() ,以下结论:①
,以下结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,其中正确的结论有__.
,其中正确的结论有__.

【答案】①③④
【解析】
根据角平分线定义得出∠ABC=2∠ABD=2∠DBC,∠EAC=2∠EAD,∠ACF
=2∠DCF,根据三角形的内角和定理得出∠BAC+ABC+∠ACB=180°,根据三角形
外角性质得出∠ACF=∠ABC+∠BAC,∠EAC=∠ABC+∠ACB,根据已知结论逐步推理
即可判断各项
①∵AD平分△ABC的外角∠EAC,
∴∠EAD=∠DAC,
∵∠EAC=∠ACB+∠ABC,且∠ABC=∠ACB,
∴∠EAD=∠ABC,
∴AD∥BC,
故①正确。
②由(1)可知AD∥BC,
∴∠ADB=∠DBC,
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∴∠ABC=2∠ADB,
∵∠ABC=∠ACB,
∴∠ACB=2∠ADB,
故②错误。
③在△ADC中,∠ADC+∠CAD+∠ACD=180°,
∵CD平分△ABC的外角∠ACF,
∴∠ACD=∠DCF
∵AD∥BC,
∴∠ADC=∠DCF,∠ADB=∠DBC,∠CAD=∠ACB
∴∠ACD=∠ADC,∠CAD=∠ACB=∠ABC=2∠ABD,
∴∠ADC+∠CAD+∠ACD=∠ADC+2∠ABD+∠ADC=2∠ADC+2∠ABD=180°,
∴∠ADC+∠ABD=90°
故③正确;
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∵∠ADB=∠DBC,
∴∠ADB=∠DBC,
∵∠DCF=90°-![]() ∠ABC=90°-∠BDC=∠DBC+∠BDC
∠ABC=90°-∠BDC=∠DBC+∠BDC
∵∠ABC=90°-∠BDC=∠DBC+∠BDC,
∴∠BDC=90°-2∠DBC,
∠DBC=45°-![]() ∠BDC,④正确
∠BDC,④正确
故选:①③④.


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=90°,AD⊥BC,∠ABC的平分线BE交AD于点F,AG平分∠DAC.给出下列结论:①∠BAD=∠C;②∠AEF=∠AFE;③∠EBC=∠C;④AG⊥EF.正确结论有( )

A. 4个B. 3个C. 2个D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
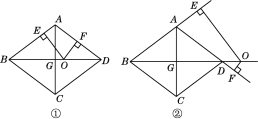
【题目】如图,在边长为10的菱形ABCD中,对角线BD=16,对角线AC,BD相交于点G,点O是直线BD上的动点,OE⊥AB于E,OF⊥AD于F.
(1)求对角线AC的长及菱形ABCD的面积.
(2)如图①,当点O在对角线BD上运动时,OE+OF的值是否发生变化?请说明理由.
(3)如图②,当点O在对角线BD的延长线上时,OE+OF的值是否发生变化?若不变,请说明理由;若变化,请探究OE,OF之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别是可活动的菱形和平行四边形学具,已知平行四边形较短的边与菱形的边长相等.
(1)在一次数学活动中,某小组学生将菱形的一边与平行四边形较短边重合,摆拼成如图1所示的图形,AF经过点C,连接DE交AF于点M,观察发现:点M是DE的中点.
下面是两位学生有代表性的证明思路:
思路1:不需作辅助线,直接证三角形全等;
思路2:不证三角形全等,连接BD交AF于点H.…
请参考上面的思路,证明点M是DE的中点(只需用一种方法证明);
(2)如图2,在(1)的前提下,当∠ABE=135°时,延长AD、EF交于点N,求![]() 的值;
的值;
(3)在(2)的条件下,若![]() =k(k为大于
=k(k为大于![]() 的常数),直接用含k的代数式表示
的常数),直接用含k的代数式表示![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在10×10的正方形网格中,每个小正方形的边长为1个单位长度.△ABC的顶点都在正方形网格的格点上,且通过两次平移(沿网格线方向作上下或左右平移)后得到△A′B′C′,点C的对应点是直线上的格点C′.

(1)画出△A′B′C′.
(2)△ABC两次共平移了___个单位长度。
(3)试在直线上画出点P,使得由点A′、B′、C′、P四点围成的四边形的面积为9.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,三角形纸片中,AB=5cm,AC=7cm,BC=9cm.沿过点B的直线折叠这个三角形,使点A落在BC边上的点E处,折痕为BD,则△DEC的周长是________cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在括号内填写理由.
如图,已知∠B+∠BCD=180°,∠B=∠D.
求证:∠E=∠DFE.

证明:∵∠B+∠BCD=180°(已知),
∴AB∥CD(______________________).
∴∠B=_______(_____________________).
又∵∠B=∠D(已知),
∴∠DCE=∠D(_____________________).
∴AD∥BE(_____________________).
∴∠E=∠DFE(_____________________).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com