
【题目】如图1,![]() ,
,![]() ,
,![]() 是郑州市二七区三个垃圾存放点,点
是郑州市二七区三个垃圾存放点,点![]() ,
,![]() 分别位于点
分别位于点![]() 的正北和正东方向,
的正北和正东方向,![]() 米,八位环卫工人分别测得的
米,八位环卫工人分别测得的![]() 长度如下表:
长度如下表:
甲 | 乙 | 丙 | 丁 | 戊 | 戌 | 申 | 辰 | |
BC(单位:米) | 84 | 76 | 78 | 82 | 70 | 84 | 86 | 80 |
他们又调查了各点的垃圾量,并绘制了下列尚不完整的统计图2,图3:
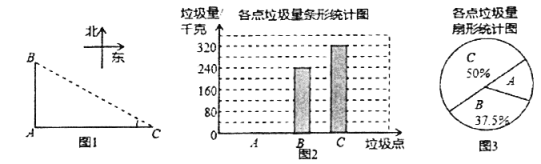
(1)求表中![]() 长度的平均数
长度的平均数![]() 、中位数、众数;
、中位数、众数;
(2)求![]() 处的垃圾量,并将图2补充完整;
处的垃圾量,并将图2补充完整;
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2+2x﹣3.
(1)写出它的顶点坐标;
(2)当x取何值时,y随x的增大而增大;
(3)求出图象与x轴的交点坐标.
(4)当x取何值时y的值大于0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商家计划从厂家采购空调和冰箱两种产品共![]() 台,空调和冰箱的采购单价与销售单价如表所示:
台,空调和冰箱的采购单价与销售单价如表所示:
采购单价 | 销售单价 | |
空调 |
|
|
冰箱 |
|
|
![]() 若采购空调
若采购空调![]() 台,且所采购的空调和冰箱全部售完,求商家的利润;
台,且所采购的空调和冰箱全部售完,求商家的利润;
![]() 厂家有规定,采购空调的数量不少于
厂家有规定,采购空调的数量不少于![]() 台,且空调采购单价不低于
台,且空调采购单价不低于![]() 元,问商家采购空调多少台时总利润最大?并求最大利润.
元,问商家采购空调多少台时总利润最大?并求最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在甲村至乙村的公路上有一块山地正在开发,现有一![]() 处需要爆破.已知点
处需要爆破.已知点![]() 与公路上的停靠站
与公路上的停靠站![]() 的距离为300米,与公路上的另一停靠站
的距离为300米,与公路上的另一停靠站![]() 的距离为400米,且
的距离为400米,且![]() ,如图所示为了安全起见,爆破点
,如图所示为了安全起见,爆破点![]() 周围半径250米范围内不得进入,问在进行爆破时,公路
周围半径250米范围内不得进入,问在进行爆破时,公路![]() 段是否因为有危险而需要暂时封锁?请说明理由.
段是否因为有危险而需要暂时封锁?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场试销一种成本为每件60元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于45%,经试销发现,销售量![]() (件)与销售单价
(件)与销售单价![]() (元)符合一次函数
(元)符合一次函数![]() ,且
,且![]() 时,
时,![]() ;
;![]() 时,
时,![]() .
.
(1)求一次函数![]() 的表达式;
的表达式;
(2)若该商场获得利润为![]() 元,试写出利润
元,试写出利润![]() 与销售单价
与销售单价![]() 之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
(3)若该商场获得利润不低于500元,试确定销售单价![]() 的范围.
的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班“数学兴趣小组”对函数y=x2﹣2|x|的图象和性质进行了探究,探究过程如下,请补充完整.
(1)自变量x的取值范围是全体实数,x与y的几组对应值列表:
x | … | ﹣3 | - | ﹣2 | ﹣1 | 0 | 1 | 2 |
| 3 | … |
y | … | 3 |
| m | ﹣1 | 0 | ﹣1 | 0 |
| 3 | … |
其中m= .
(2)根据上表数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该函数图象的另一部分;
(3)观察函数图象,写出2条函数的性质;
(4)进一步探究函数图象发现:
①函数图象与x轴有 个交点,所对应的方程x2﹣2|x|=0有
②方程x2﹣2|x|=2有 个实数根.
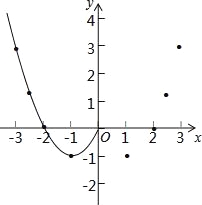
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰三角形![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 边的中点,点
边的中点,点![]() 在线段
在线段![]() 上从
上从![]() 向
向![]() 运动,同时点
运动,同时点![]() 在线段
在线段![]() 上从点
上从点![]() 向
向![]() 运动,速度都是1个单位/秒,时间是
运动,速度都是1个单位/秒,时间是![]() (
(![]() ),连接
),连接![]() 、
、![]() 、
、![]() .
.

(1)请判断![]() 形状,并证明你的结论.
形状,并证明你的结论.
(2)以![]() 、
、![]() 、
、![]() 、
、![]() 四点组成的四边形面积是否发生变化?若不变,求出这个值:若变化,用含
四点组成的四边形面积是否发生变化?若不变,求出这个值:若变化,用含![]() 的式子表示.
的式子表示.
查看答案和解析>>
科目:初中数学 来源: 题型:
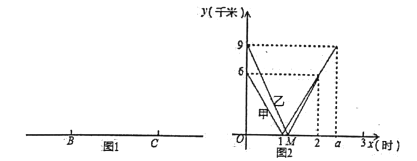
【题目】如图![]() ,一条笔直的公路上有
,一条笔直的公路上有![]() 、
、![]() 、
、![]() 三地
三地![]() 、
、![]() 两地相距
两地相距![]() 千米,甲、乙两个野外徒步爱好小组从
千米,甲、乙两个野外徒步爱好小组从 ![]() 、
、![]() 两地同时出发,沿公路始终匀速相向而行,分别走向
两地同时出发,沿公路始终匀速相向而行,分别走向![]() 、
、![]() 两地.甲、乙两组到
两地.甲、乙两组到![]() 地的距离
地的距离![]() ,
,![]() (千米)与行走时间
(千米)与行走时间![]() (时)的关系如图
(时)的关系如图![]() 所示.
所示.
(1)请在图![]() 中标出
中标出![]() 地的位置,并写出相应的距离:
地的位置,并写出相应的距离:![]()
![]() ;
;
(2)在图![]() 中求出甲组到达
中求出甲组到达![]() 地的时间
地的时间![]() ;
;
(3)求岀乙组从![]() 地到
地到![]() 地行走过程中
地行走过程中![]() 与行走时间
与行走时间![]() 的关系式.
的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
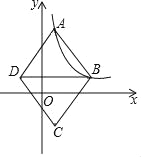
【题目】如图,在平面直角坐标系中,菱形ABCD的顶点A、B在反比例函数y=![]() (k>0,x>0)的图象上,横坐标分别为1,4,对角线BD∥x轴.若菱形ABCD的面积为
(k>0,x>0)的图象上,横坐标分别为1,4,对角线BD∥x轴.若菱形ABCD的面积为![]() ,则k的值为_____.
,则k的值为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com