
【题目】在平面直角坐标系中,点O为坐标原点,抛物线y=ax2+bx+c与x轴交于点A(-1,0),B(3,0),与y轴交于点C(0,3),顶点为G.
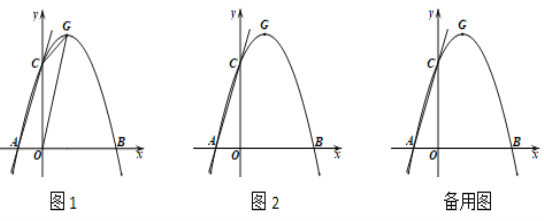
(1)求抛物线和直线AC的解析式;
(2)如图1,设E(m,0)为x正半轴上的一个动点,若△CGE和△CGO的面积满足S△CGE=![]() S△CGO,求点E的坐标;
S△CGO,求点E的坐标;
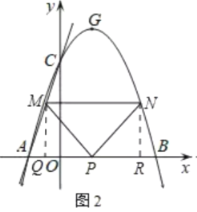
(3)如图2,设点P从点A出发,以每秒1个单位长度的速度沿x轴向右运动,运动时间为ts,点M为射线AC上一动点,过点M作MN∥x轴交抛物线对称轴右侧部分于点N.试探究点P在运动过程中,是否存在以P,M,N为顶点的三角形为等腰直角三角形,若存在,求出t的值;若不存在,请说明理由.
【答案】(1)![]() ;y=3x+3;(2)点E的坐标为:(1,0)或(-7,0);(3)存在,t的值为
;y=3x+3;(2)点E的坐标为:(1,0)或(-7,0);(3)存在,t的值为![]() 或
或![]() 或
或![]() .
.
【解析】
(1)用待定系数法即能求出抛物线和直线AC解析式.
(2)△CGE与△CGO虽然有公共底边CG,但高不好求,故把△CGE构造在比较好求的三角形内计算.延长GC交x轴于点F,则△FGE与△FCE的差即为△CGE.
(3)设M的坐标(e,3e+3),分别以M、N、P为直角顶点作分类讨论,利用等腰直角三角形的特殊线段长度关系,用e表示相关线段并列方程求解,再根据e与AP的关系求t的值.
解:(1)将点A(-1,0),B(3,0),点C(0,3)代入抛物线y=ax2+bx+c得,
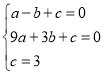 ,解得
,解得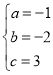 ,
,
∴![]() ,
,
设直线AC的解析式为y=kx+n,
将点A(-1,0),点C(0,3)代入得:![]() ,解得:k=3,n=3
,解得:k=3,n=3
∴直线AC的解析式为:y=3x+3
(2)延长GC交x轴于点F,过点G作GH⊥x轴于点H,
∵![]()
∴G(1,4),GH=4,
∴![]() ,
,
若S△CGE=![]() S△CGO,
S△CGO,
则S△CGE=![]() S△CGO=
S△CGO=![]() ,
,
①若点E在x轴的正半轴,
设直线CG为![]() ,将G(1,4)代入得
,将G(1,4)代入得![]()
∴![]() ,
,
∴直线CG的解析式为y=x+3,
∴当y=0时,x=-3,即F(-3,0)
∵E(m,0)
∴EF=m-(-3)=m+3
∴![]()
=![]()
= ![]()
=![]()
=![]()
∴![]() ,解得:m=1
,解得:m=1
∴E的坐标为(1,0)
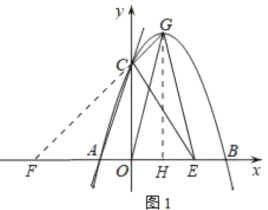
②若点E在x轴的负半轴上,则点E到直线CG的距离与点(1,0)到直线CG的距离相等,
即点E到点F的距离等于点(1,0)到点F的距离,
∴EF=-3-m=1-(-3)=4
∴m=-7,即E(-7,0)
综上所述,点E的坐标为:(1,0)或(-7,0)
(3)存在以P,M,N为顶点的三角形为等腰直角三角形,
设M(e,3e+3),e>-1,则![]() ,
,
①如图2,若∠MPN=90°,PM=PN,
过点M作MQ⊥x轴于点Q,过N作NR⊥x轴于点R,
∵MN∥x轴
∴MQ=NR=3e+3
∴Rt△MQP≌Rt△NRP(HL)
∴PQ=PR,∠MPQ=∠NPR=45°
∴MQ=PQ=PR=NR=3e+3
∴xN=xM+3e+3+3e+3=7e+6,即N(7e+6,3e+3)
∵N在抛物线上
∴(7e+6)2+2(7e+6)+3=3e+3,
解得:![]() (舍去),
(舍去),![]()
∵AP=t,OP=t1,OP+OQ=PQ
∴t1e=3e+3
∴t=4e+4=![]() ,
,
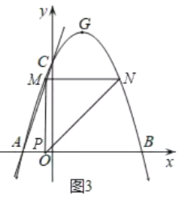
②如图3,若∠PMN=90°,PM=MN,
∴MN=PM=3e+3
∴xN=xM+3e+3=4e+3,即N(4e+3,3e+3)
∴(4e+3)2+2(4e+3)+3=3e+3
解得:e1=1(舍去),e2=![]() ,
,
∴t=AP=e(1)=,
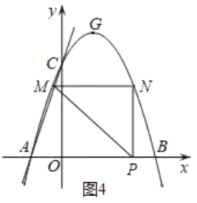
③如图4,若∠PNM=90°,PN=MN,
∴MN=PN=3e+3,N(4e+3,3e+3)
解得:e=![]()
∴t=AP=OA+OP=1+4e+3=![]()
综上所述,存在以P,M,N为顶点的三角形为等腰直角三角形,t的值为![]() 或
或![]() 或
或![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】为了迎接疫情彻底结束后的购物高峰,某运动品牌专卖店准备购进甲、乙两种运动鞋.其中甲、乙两种运动鞋的进价和售价如下表:
运动鞋价格 | 甲 | 乙 |
进价(元/双) | m | m﹣20 |
售价(元/双) | 240 | 160 |
已知:用3000元购进甲种运动鞋的数量与用2400元购进乙种运动鞋的数量相同.
(1)求m的值;
(2)要使购进的甲、乙两种运动鞋共200双的总利润(利润=售价﹣进价)不少于21700元,且甲种运动鞋的数量不超过100双,问该专卖店共有几种进货方案?
(3)在(2)的条件下,专卖店准备对甲种运动鞋进行优惠促销活动,决定对甲种运动鞋每双优惠a(50<a<70)元出售,乙种运动鞋价格不变.那么该专卖店要获得最大利润应如何进货?
查看答案和解析>>
科目:初中数学 来源: 题型:
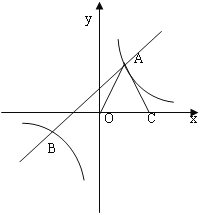
【题目】如图,反比例函数![]() 与一次函数
与一次函数![]() 的图象交于两点A(1,3)、B(n,-1).
的图象交于两点A(1,3)、B(n,-1).
(1)求这两个函数的解析式;
(2)观察图象,请直接写出不等式![]() 的解集;
的解集;
(3)点C为x轴正半轴上一点,连接AO、AC,且AO=AC,求⊿AOC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知BC⊥AC,圆心O在AC上,点M与点C分别是AC与⊙O的交点,点D是MB与⊙O的交点,点P是AD延长线与BC的交点,且ADAO=AMAP.
(1)连接OP,证明:△ADM∽△APO;
(2)证明:PD是ΘO的切线;
(3)若AD=24,AM=MC,求![]() 的值.
的值.
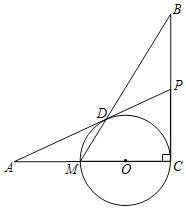
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=mx+n(m≠0)的图象与y轴交于点C,与反比例函数y=![]() (k≠0)的图象交于A,B两点,点A在第一象限,纵坐标为4,点B在第三象限,BM⊥x轴,垂足为点M,BM=OM=2.
(k≠0)的图象交于A,B两点,点A在第一象限,纵坐标为4,点B在第三象限,BM⊥x轴,垂足为点M,BM=OM=2.

(1)求反比例函数和一次函数的解析式.
(2)连接OB,MC,求四边形MBOC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a>0)图象的顶点为点D,其图象与x轴的交点A,B的横坐标分别为﹣1和3,给出下列结论:①2a﹣b=0;②a+b+c<0;③3a+c=0;④当a=![]() 时,△ABD是等腰直角三角形.其中,正确的结论有( )
时,△ABD是等腰直角三角形.其中,正确的结论有( )
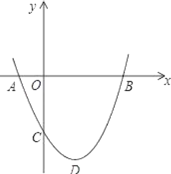
A.①②③B.③④C.②③④D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线:y=x2+2(a-1)x+a2-2a(a>0), P(2,3)在此抛物线上
(1)求该抛物线的解析式
(2)求直线 y=2x-2 与此抛物线的公共点个数;若有公共点,求出公共点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(3分)如图,△ABC中,AB=AC,AB的垂直平分线交边AB于D点,交边AC于E点,若△ABC与△EBC的周长分别是40cm,24cm,则AB= cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
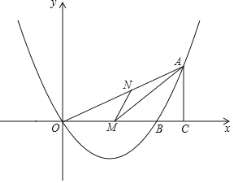
【题目】如图,已知二次函数 y=ax2+bx 的图象与 x 轴交于点 O(0,0)和 点 B,抛物线的对称轴是直线 x=3.点 A 是抛物线在第一象限上的一个动点, 过点 A 作 AC⊥x 轴,垂足为 C.S△AOB=3S△ABC,AC2=OCBC.
(1)求该二次函数的解析式;
(2)抛物线的对称轴与 x 轴交于点 M.连接 AM,点 N 是线段 OA 上的一点.当 ∠AMN=∠AOM 时,求点 N 的坐标;
(3)点 P 是抛物线上的一个动点.点 Q 是 y 轴上的一动点.当以 A,B,P,Q 四个点为顶点的四边形为平行四边形时,直接写出点 P 坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com