
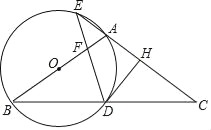
【题目】如图,在△ABC中,AB=AC,以AB为直径作圆O,分别交BC于点D,交CA的延长线于点E,过点D作DH⊥AC于点H,连接DE交线段OA于点F.
(1)求证:DH是圆O的切线;
(2)若A为EH的中点,求![]() 的值;
的值;
(3)若EA=EF=1,求圆O的半径.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]()
【解析】试题分析:(1)根据同圆的半径相等和等边对等角证明:∠ODB=∠OBD=∠ACB,则DH⊥OD,DH是圆O的切线;
(2)如图2,先证明∠E=∠B=∠C,则H是EC的中点,设AE=x,EC=4x,则AC=3x,由OD是△ABC的中位线,得:OD=![]() AC=
AC=![]() ,证明△AEF∽△ODF,列比例式可得结论;
,证明△AEF∽△ODF,列比例式可得结论;
(3)如图2,设⊙O的半径为r,即OD=OB=r,证明DF=OD=r,则DE=DF+EF=r+1,BD=CD=DE=r+1,证明△BFD∽△EFA,列比例式为:![]() ,则
,则![]() ,求出r的值即可.
,求出r的值即可.
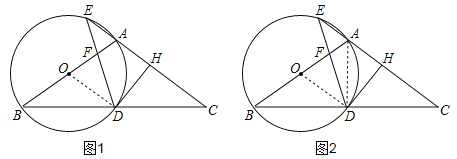
(1)连接OD,如图1,∵OB=OD,∴△ODB是等腰三角形,∠OBD=∠ODB①,在△ABC中,∵AB=AC,∴∠ABC=∠ACB②,由①②得:∠ODB=∠OBD=∠ACB,∴OD∥AC,∵DH⊥AC,∴DH⊥OD,∴DH是圆O的切线;
(2)如图2,在⊙O中,∵∠E=∠B,∴由(1)可知:∠E=∠B=∠C,∴△EDC是等腰三角形,∵DH⊥AC,且点A是EH中点,设AE=x,EC=4x,则AC=3x,连接AD,则在⊙O中,∠ADB=90°,AD⊥BD,∵AB=AC,∴D是BC的中点,∴OD是△ABC的中位线,∴OD∥AC,OD=![]() AC=
AC=![]() ,∵OD∥AC,∴∠E=∠ODF,在△AEF和△ODF中,∵∠E=∠ODF,∠OFD=∠AFE,∴△AEF∽△ODF,∴
,∵OD∥AC,∴∠E=∠ODF,在△AEF和△ODF中,∵∠E=∠ODF,∠OFD=∠AFE,∴△AEF∽△ODF,∴![]() ,∴
,∴![]() =
=![]() ,∴
,∴![]() =
=![]() ;
;
(3)如图2,设⊙O的半径为r,即OD=OB=r,∵EF=EA,∴∠EFA=∠EAF,∵OD∥EC,∴∠FOD=∠EAF,则∠FOD=∠EAF=∠EFA=∠OFD,∴DF=OD=r,∴DE=DF+EF=r+1,∴BD=CD=DE=r+1,在⊙O中,∵∠BDE=∠EAB,∴∠BFD=∠EFA=∠EAB=∠BDE,∴BF=BD,△BDF是等腰三角形,∴BF=BD=r+1,∴AF=AB﹣BF=2OB﹣BF=2r﹣(1+r)=r﹣1,在△BFD和△EFA中,∵∠BDF=∠EFA,∠B=∠E,∴△BFD∽△EFA,∴![]() ,∴
,∴![]() ,解得:r1=
,解得:r1=![]() ,r2=
,r2=![]() (舍),综上所述,⊙O的半径为
(舍),综上所述,⊙O的半径为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图1,在锐角△ABC中,∠ABC=45°,高线AD、BE相交于点F.
(1)判断BF与AC的数量关系并说明理由;
(2)如图2,将△ACD沿线段AD对折,点C落在BD上的点M,AM与BE相交于点N,当DE∥AM时,判断NE与AC的数量关系并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中的△ABC,若小方格边长为1,格点△ABC(顶点是网格线交点的三角形)的顶点A,C的坐标分别为(﹣1,1),(0,﹣2),请你根据所学的知识.
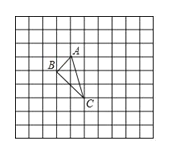
(1)在如图所示的网格平面内作出平面直角坐标系;
(2)作出△ABC关于y轴对称的三角形A1B1C1;
(3)判断△ABC的形状,并求出△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
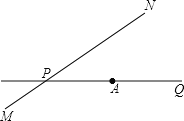
【题目】如图,公路MN和公路PQ在点P处交汇,且∠QPN=30°,点A处有一所中学,AP=160m.若拖拉机行驶时,周围100m以内会受到噪音的影响,那么拖拉机在公路MN上沿PN方向行驶时:
(1)学校是否会受到噪声影响?
(2)如果不受影响,请说明理由;如果受影响,已知拖拉机的速度为18km/h,那么学校受影响的时间为多少秒?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,![]() ,
,![]() ,直线
,直线![]() 经过点
经过点![]() ,且
,且![]() 于
于![]() ,
,![]() 于
于![]() .
.
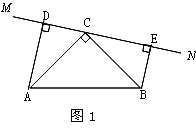
(1)当直线![]() 绕点
绕点![]() 旋转到图1的位置时,
旋转到图1的位置时,
①求证:△ADC≌△CEB.
②求证:DE=AD+BE.
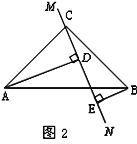
(2)当直线![]() 绕点
绕点![]() 旋转到图2的位置时,判断
旋转到图2的位置时,判断![]() 和
和![]() 的关系,并说明理由.
的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【操作发现】
如图①,在边长为1个单位长度的小正方形组成的网格中,△ABC的三个顶点均在格点上.

(1)请按要求画图:将△ABC绕点A按顺时针方向旋转90°,点B的对应点为B′,点C的对应点为C′,连接BB′;
(2)在(1)所画图形中,∠AB′B= .
【问题解决】
如图②,在等边三角形ABC中,AC=7,点P在△ABC内,且∠APC=90°,∠BPC=120°,求△APC的面积.
小明同学通过观察、分析、思考,对上述问题形成了如下想法:
想法一:将△APC绕点A按顺时针方向旋转60°,得到△AP′B,连接PP′,寻找PA,PB,PC三条线段之间的数量关系;
想法二:将△APB绕点A按逆时针方向旋转60°,得到△AP′C′,连接PP′,寻找PA,PB,PC三条线段之间的数量关系.
…
请参考小明同学的想法,完成该问题的解答过程.(一种方法即可)
【灵活运用】
如图③,在四边形ABCD中,AE⊥BC,垂足为E,∠BAE=∠ADC,BE=CE=2,CD=5,AD=kAB(k为常数),求BD的长(用含k的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,O是AB的中点,连接DO并延长交CB的延长线于点E,连接AE、DB.
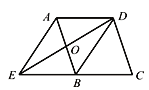
(1)求证:△AOD≌△BOE;
(2)若DC=DE,判断四边形AEBD的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com