练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    若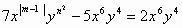，求m、n的值．

    解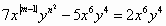：∵，则与是同类项，

    ∴=6，，∴．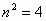

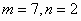    观察本题的解法是否正确，如果错误，请写出正确解法．

    答案：
    解析：

    此解错误．

    正确解法：由已知得=6，，即m－1=6或m－1=－6，，

    ∴m=7或m=－5，．


    提示：

    此解错在最后一步，因为互为相反数的绝对值相等，平方也相等，因此由=6，得m－1=6或m－1=－6，由，得．此错属于性质运用不当．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    （2013•济南一模）如图，已知矩形ABCD中，AB=8cm，BC=6cm，如果点P由C出发沿CA方向向点A匀速运动，同时点Q由A出发沿AB方向向点B匀速运动，它们的速度均为2cm/s，连接PQ，设运动的时间为t．（单位：s）．（0≤t≤4）解答下列问题：
    （1）求AC的长；
    （2）当t为何值时，PQ∥BC；
    （3）设△AQP的面积为S（单位：cm2），当t为何值时，s=
    365
    cm2；
    （4）是否存在某时刻t，使线段PQ恰好把△ABC的面积平分？若存在求出此时t的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，已知△ABC中，AB=10cm，AC=8cm，BC=6cm，如果点P由B出发沿BA方向向点A匀速运动，速度为2cm/s，同时点Q由A出发沿AC方向向点C匀速运动，速度为1cm/s，连接PQ，设运动的时间为t（单位：s）（0≤t≤5）．解答下列问题：
    （1）当t为何值时，△APQ是直角三角形？
    （2）是否存在某时刻t，使线段PQ恰好把△ABC的面积平分？若存在求出此时t的值；若不存在，请说明理由；
    （3）把△APQ沿AB（或沿AC）翻折，翻折前后的两个三角形所组成的四边形能不能是菱形？若能，求出此时菱形的面积；若不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    有一人患了流感，经过两轮传染后共有144人患了流感，问：
    （1）每轮传染中平均一个人传染了几个人？
    （2）按照这样的速度，三轮传染后有多少人患流感？
    （3）设前n轮传染的平均数为S1，前n-1轮传染的平均数为S2，是否存在一个正整数K，使S1=KS2？若存在求出所有K的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知抛物线经过点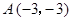和点P （t，0），且t ≠ 0
    【小题1】若该抛物线的对称轴经过点A，如图，请通过观察图象，指出此时y的最小值，并写出t的值；

    【小题2】若，求a、b的值，并指出此时抛物线的开口方向
    【小题3】直接写出使该抛物线开口向下的t的一个值

    查看答案和解析>>

    科目：初中数学 来源：2014界湖北省初三上学期期末模拟数学试卷（解析版） 题型：解答题

    如图所示,某居民小区要在一块一边靠墙（墙长15m）的空地上修建一个矩形花园ABCD,花园的一边靠墙,另三边用总长为40m的栅栏围成,若花园的BC边长为x米,花园的面积为y（m2）

    （1）求y与x之间的函数关系式,并写出自变量x的取值范围;

    （2）满足条件的花园面积能达到200m2吗？若能,求出此时x的值;若不能,说明理由;

    （3）请结合题意,判断当x取何值时,花园的面积最大？

     

    查看答案和解析>>

    同步练习册答案