
 如图,已知在平面直角坐标系xOy中,抛物线y=
如图,已知在平面直角坐标系xOy中,抛物线y=| 1 |
| 4 |
| 1 |
| 4 |

| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |

| 2 |
|
|
| 1 |
| 2 |
| 2 |
| 2 |
| NE |
| AE |
| ||
3
|
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 1 |
| 3 |
| AH |
| tan∠AD2H |
| 1 |
| 3 |
| 4 |
| 3 |


科目:初中数学 来源: 题型:
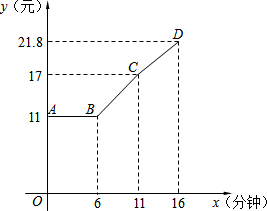 某市出租车按里程计费标准为:不超过3公里部分,计费11元,超过3公里部分,按每公里2.4元计费.现在在此基础上,如果车速不超过12公里/小时,那么再加收0.48元/分钟,这项费用叫做“双计费”.图中三段折线表示某时间段内,一辆出租车的计费总额y(元)与行驶时间x(分钟)的函数关系(出租车在每段上均匀速行驶).
某市出租车按里程计费标准为:不超过3公里部分,计费11元,超过3公里部分,按每公里2.4元计费.现在在此基础上,如果车速不超过12公里/小时,那么再加收0.48元/分钟,这项费用叫做“双计费”.图中三段折线表示某时间段内,一辆出租车的计费总额y(元)与行驶时间x(分钟)的函数关系(出租车在每段上均匀速行驶).查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在平面直角坐标系中,直线l是第二、四象限的角平分线.
如图,在平面直角坐标系中,直线l是第二、四象限的角平分线.查看答案和解析>>
科目:初中数学 来源: 题型:
 已知:如图,在梯形ABCD中,AD∥BC,∠ABC=90°,BC=2AD,点E是BC的中点、F是CD上的点,联结AE、EF、AC.
已知:如图,在梯形ABCD中,AD∥BC,∠ABC=90°,BC=2AD,点E是BC的中点、F是CD上的点,联结AE、EF、AC.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,直线PD垂直平分⊙O的半径OA于点B,PD交⊙O于点C、D,PE是⊙O的切线,E为切点,连结AE,交CD于点F.
如图,直线PD垂直平分⊙O的半径OA于点B,PD交⊙O于点C、D,PE是⊙O的切线,E为切点,连结AE,交CD于点F.查看答案和解析>>
科目:初中数学 来源: 题型:
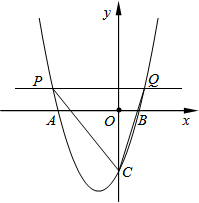 如图,在平面直角坐标系xOy中,二次函数y=ax2+bx-3(a,b是常数)的图象与x轴交于点A(-3,0)和点B(1,0),与y轴交于点C.动直线y=t(t为常数)与抛物线交于不同的两点P、Q.
如图,在平面直角坐标系xOy中,二次函数y=ax2+bx-3(a,b是常数)的图象与x轴交于点A(-3,0)和点B(1,0),与y轴交于点C.动直线y=t(t为常数)与抛物线交于不同的两点P、Q.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com