
分析 (1)原式变形后,利用平方差公式计算即可;
(2)此题不难发现:3n的个位数字是3,9,7,1四个一循环,所以(3+1)(32+1)(34+1)(38+1)(316+1)的个位是0,则2(3+1)(32+1)(34+1)(38+1)(316+1)+37的个位是0,从而得到结果;
(3)根据平方差公式求出即可.
解答 解:(1)原式=(2-1)(2+1)(22+1)(24+1)…(2n+1)+1
=(22-1)(22+1)(24+1)…(2n+1)+1
=(24-1)(24+1)…(2n+1)+1
=22n-1+1
=22n;∵24=16,28=(24)2=256,216=(28)2=65536….
∴22n的尾数为6;
故答案为:6,
(2)∵31=3,32=9,33=27,34=81,35=243,36=729,…,
∵3n的个位数字是3,9,7,1四个一循环,
∴(3+1)(32+1)(34+1)(38+1)(316+1)的个位是0,
∴2(3+1)(32+1)(34+1)(38+1)(316+1)+37的个位是0,
∴2(3+1)(32+1)(34+1)(38+1)(316+1)+1的个位数字是0+1=1;
故答案为:1;
(3)2(3+1)(32+1)(34+1)(38+1)+1=(3-1)(3+1)(32+1)(34+1)(38+1)+1
=(38-1)(38+1)+1
=316-1+1=316.
点评 此题主要考查了平方差公式,熟练应用平方差公式是解题关键.


科目:初中数学 来源: 题型:解答题
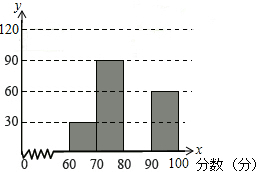 某校举行了一场学生“安全知识”问答竞赛活动,为了解笔试情况,随机抽查了部分学生的得分情况,请根据图表提供的信息,解答下列问题:
某校举行了一场学生“安全知识”问答竞赛活动,为了解笔试情况,随机抽查了部分学生的得分情况,请根据图表提供的信息,解答下列问题:| 分数段 | 频数 | 频率 |
| 60≤x<70 | 30 | 0.1 |
| 70≤x<80 | 90 | n |
| 80≤x<90 | m | 0.4 |
| 90≤x<100 | 60 | 0.2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
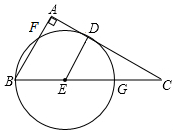 如图,在Rt△ABC中,∠A=90°,点D、E分别在AC、BC上,且CD•BC=AC•CE,以E为圆心,DE长为半径作圆,⊙E经过点B,与AB、BC分别交于点F、G.
如图,在Rt△ABC中,∠A=90°,点D、E分别在AC、BC上,且CD•BC=AC•CE,以E为圆心,DE长为半径作圆,⊙E经过点B,与AB、BC分别交于点F、G.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
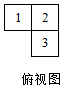 由6个大小相同的小正方体组合成一个几何体,其俯视图如图所示,其中正方形中的数字表示该位置放置的小正方体的个数,则该几何体的左视图为( )
由6个大小相同的小正方体组合成一个几何体,其俯视图如图所示,其中正方形中的数字表示该位置放置的小正方体的个数,则该几何体的左视图为( )| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com