
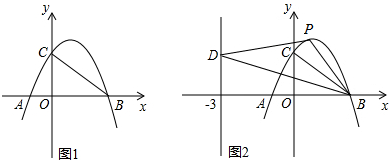
·ÖĪö £Ø1£©ĄūÓĆÅ×ĪļĻߵĶŌ³ĘŠŌæÉĒóµĆµćAµÄ×ų±ź£¬ÉčÅ×ĪļĻߵĽāĪöŹ½ĪŖy=a£Øx+1£©£Øx-3£©£¬½«µćCµÄ×ų±ź“śČėæÉĒóµĆaµÄÖµ£»
£Ø2£©ĻČĒóµĆÖ±ĻßBCµÄ½āĪöŹ½£¬Č»ŗóĒóµĆµ±x=1Ź±£¬¶ŌÓ¦µÄŗÆŹżÖµ£¬Ę½ŅĘŗóÅ×ĪļĻߵĽāĪöŹ½ĪŖy=-£Øx-1£©2+4-d£®Å×ĪļĻߵĶ„µćŌŚ”÷OBCµÄÄŚ²æ£Ø°üĄØ”÷OBCµÄ±ß½ē£©£¬Ōņ0”Ü4-d”Ü2£»
£Ø3£©¹żµćP×÷PE”ĶyÖį£¬½»Ö±Ļßx=-3ÓėµćE£¬¹żµćB×÷BF”ĶPE£¬“¹×ćĪŖF£®ĻČÖ¤Ć÷”÷EPD”Õ”÷FBP£¬ŅĄ¾ŻČ«µČČż½ĒŠĪµÄŠŌÖŹæɵƵ½EP=FB£®ÉčµćPµÄ×ų±źĪŖ£Øx£¬-x2+2x+3£©£¬ŌņPE=x+3£¬FB=|-x2+2x+3|£¬Č»ŗóŅĄ¾ŻPE=FBæɵƵ½¹ŲÓŚxµÄ·½³Ģ£¬Č»ŗóæÉĒóµĆxµÄÖµ£¬“Ó¶ųæɵƵ½µćPµÄ×ų±ź£®
½ā“š ½ā£ŗ£Ø1£©”ßB£Ø3£¬0£©£¬¶Ō³ĘÖįĪŖÖ±Ļßx=1£¬
”ąA£Ø-1£¬0£©£®
ÉčÅ×ĪļĻߵĽāĪöŹ½ĪŖy=a£Øx+1£©£Øx-3£©£¬½«µćCµÄ×ų±ź“śČėµĆ£ŗ-3a=3£¬½āµĆ£ŗa=-1£¬
”ąÅ×ĪļĻߵĽāĪöŹ½ĪŖy=-x2+2x+3£®
£Ø2£©ÉčÖ±ĻßBCµÄ½āĪöŹ½ĪŖy=kx+3£¬½«µćBµÄ×ų±ź“śČėµĆ£ŗ3k+3=0£¬½āµĆk=-1£¬
”ąÖ±ĻßBCµÄ½āĪöŹ½ĪŖy=-x+3£®
µ±x=1Ź±£¬y=2£®
”ßy=-x2+2x+3=-£Øx-1£©2+4£¬
”ąĘ½ŅĘŗóÅ×ĪļĻߵĽāĪöŹ½ĪŖy=-£Øx-1£©2+4-d£®
”ßÅ×ĪļĻߵĶ„µćŌŚ”÷OBCµÄÄŚ²æ£Ø°üĄØ”÷OBCµÄ±ß½ē£©£¬
”ą0”Ü4-d”Ü2£¬
”ą2”Üd”Ü4£®
£Ø3£©ČēĶ¼£ŗ¹żµćP×÷PE”ĶyÖį£¬½»Ö±Ļßx=-3ÓėµćE£¬¹żµćB×÷BF”ĶPE£¬“¹×ćĪŖF£®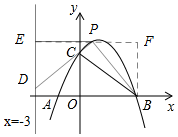
”ß”÷BPDŹĒŅŌPĪŖ¶„µćµÄµČŃüÖ±½ĒČż½ĒŠĪ£¬
”ą”ĻDPB=90”ć£¬DP=PB£®
”ą”ĻEPD+”ĻFPB=90”ć£®
Ó֔ߔĻEPD+”ĻEDP=90”ć£¬
”ą”ĻFPB=”ĻEDP£®
ŌŚ”÷EPDŗĶ”÷FBPÖŠ£¬$\left\{\begin{array}{l}{”ĻFPB=”ĻEDP}\\{”ĻPED=”ĻPFB}\\{DP=PB}\end{array}\right.$£¬
”ą”÷EPD”Õ”÷FBP£®
”ąEP=FB£®
ÉčµćPµÄ×ų±źĪŖ£Øx£¬-x2+2x+3£©£¬ŌņPE=x+3£¬FB=|-x2+2x+3|£¬
”ąx+3=|-x2+2x+3|£®
”ąx+3=-x2+2x+3»ņx+3=x2-2x-3£®
½āµĆ£ŗx=0»ņx=1»ņx=$\frac{3+\sqrt{33}}{2}$»ņx=$\frac{3-\sqrt{33}}{2}$£®
µ±x=0Ź±£¬y=3£¬
”ąP£Ø0£¬3£©£®
µ±x=1Ź±£¬y=4£®
”ąP£Ø1£¬4£©£®
µ±x=$\frac{3+\sqrt{33}}{2}$Ź±£¬y=$\frac{-\sqrt{33}-9}{2}$£¬
”ąP£Ø$\frac{3+\sqrt{33}}{2}$£¬$\frac{-\sqrt{33}-9}{2}$£©£®
µ±x=$\frac{3-\sqrt{33}}{2}$Ź±£¬y=$\frac{\sqrt{33}-9}{2}$£®
”ąP£Ø$\frac{3-\sqrt{33}}{2}$£¬$\frac{\sqrt{33}-9}{2}$£©£®
×ŪÉĻĖłŹö£¬µćPµÄ×ų±źĪŖP£Ø0£¬3£©»ņP£Ø1£¬4£©»ņP£Ø$\frac{3+\sqrt{33}}{2}$£¬$\frac{-\sqrt{33}-9}{2}$£©»ņP£Ø$\frac{3-\sqrt{33}}{2}$£¬$\frac{\sqrt{33}-9}{2}$£©£®
µćĘĄ ±¾ĢāÖ÷ŅŖæ¼²éµÄŹĒ¶ž“ĪŗÆŹżµÄ×ŪŗĻÓ¦ÓĆ£¬½ā“š±¾ĢāÖ÷ŅŖÓ¦ÓĆĮĖ“ż¶ØĻµŹż·ØĒóŅ»“ĪŗÆŹż”¢¶ž“ĪŗÆŹżµÄ½āĪöŹ½”¢Č«µČČż½ĒŠĪµÄŠŌÖŹŗĶÅŠ¶Ø£¬¹¹ŌģČ«µČČż½ĒŠĪ£¬ĄūÓĆPE=BFĮŠ³ö¹ŲÓŚxµÄ·½³ĢŹĒ½āĢāµÄ¹Ų¼ü£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
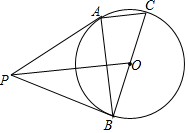 ČēĶ¼£¬PĪŖ”ŃOĶāŅ»µć£¬BCŹĒ”ŃOµÄÖ±¾¶£¬CAĪŖ”ŃOµÄŅ»ĢõĻŅ£¬Į¬½ÓPA”¢PB£¬”ĻPBA=”ĻC£®
ČēĶ¼£¬PĪŖ”ŃOĶāŅ»µć£¬BCŹĒ”ŃOµÄÖ±¾¶£¬CAĪŖ”ŃOµÄŅ»ĢõĻŅ£¬Į¬½ÓPA”¢PB£¬”ĻPBA=”ĻC£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
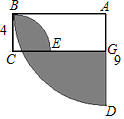 ŅŌAĪŖŌ²ŠÄ£¬°ė¾¶ĪŖ9µÄĖÄ·ÖÖ®Ņ»Ō²£¬ÓėŅŌCĪŖŌ²ŠÄ£¬°ė¾¶ĪŖ4µÄĖÄ·ÖÖ®Ņ»Ō²ČēĶ¼ĖłŹ¾·ÅÖĆ£¬ĒŅ”ĻABC=90”ć£¬ŌņĶ¼ÖŠŅõÓ°²æ·ÖµÄĆ껿ĪŖ$\frac{97}{4}$¦Š-36£®
ŅŌAĪŖŌ²ŠÄ£¬°ė¾¶ĪŖ9µÄĖÄ·ÖÖ®Ņ»Ō²£¬ÓėŅŌCĪŖŌ²ŠÄ£¬°ė¾¶ĪŖ4µÄĖÄ·ÖÖ®Ņ»Ō²ČēĶ¼ĖłŹ¾·ÅÖĆ£¬ĒŅ”ĻABC=90”ć£¬ŌņĶ¼ÖŠŅõÓ°²æ·ÖµÄĆ껿ĪŖ$\frac{97}{4}$¦Š-36£®²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com