
【题目】观察下面的变形规律:
![]() ;
;![]() ;
;![]() ;….
;….
解答下面的问题:
(1)仿照上面的格式请写出![]() = ;
= ;
(2)若n为正整数,请你猜想![]() = ;
= ;
(3)基础应用:计算:![]() .
.
(4)拓展应用1:解方程:![]() =2016
=2016
(5)拓展应用2:计算:![]() .
.
科目:初中数学 来源: 题型:
【题目】如图,点A在双曲线y= ![]() 上,点B在双曲线y=
上,点B在双曲线y= ![]() (k≠0)上,AB∥x轴,过点A作AD⊥x轴于D.连接OB,与AD相交于点C,若AC=2CD,则k的值为( )
(k≠0)上,AB∥x轴,过点A作AD⊥x轴于D.连接OB,与AD相交于点C,若AC=2CD,则k的值为( ) 
A.6
B.9
C.10
D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知正方形的边长为4,甲、乙两动点分别从正方形ABCD的顶点A、C同时沿正方形的边开始移动,甲点依顺时针方向环行,乙点依逆时针方向环行,若乙的速度是甲的速度的3倍,则它们第2018次相遇在边 ( )上.
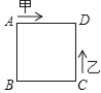
A. AB B. BC C. CD D. DA
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠A=120°,BC=6cm,AB的垂直平分线交BC于点M,交AB于点E,AC的垂直平分线交BC于点N,交AC于点F,则MN的长为( ) 
A.4cm
B.3cm
C.2cm
D.1cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地上网有两种收费方式,用户可以任选其一:
(A)记时制:2.8元/小时,
(B)包月制:16元/月.此外,每一种上网方式都加收通讯费1.2元/小时.
(1)某用户上网20小时,选用哪种上网方式比较合算?
(2)当上网时间在什么小时时,两种上网费用一样多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)化简: ![]() (2)解方程:
(2)解方程:![]() .
.
【答案】(1) ![]() 或
或![]() ;(2)x=-2.
;(2)x=-2.
【解析】(1)先把括号内通分,再把除法转化为乘法,并把分子、分母分解因式约分化简;
(2)两边都乘以最简公分母2(x+3),把分式方程化为整式方程求解,求出x的值不要忘记检验.
(1)原式=![]() =
=![]() =
=![]() 或
或![]() ;
;
(2)解:去分母得:![]() ,
,
解得:x=﹣2,
经检验x=﹣2是分式方程的解,
∴原方程的解为x=﹣2
点睛:本题考查了分式的混合运算和解分式方程,熟练掌握分式的运算法则和解分式方程的方法是解答本题的关键.
【题型】解答题
【结束】
20
【题目】小张同学学完统计知识后,随机调查了她所在辖区若干名居民的年龄,将调查数据绘制成如下扇形统计图和条形统计图:
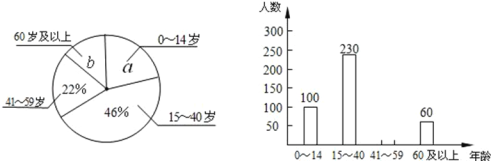
请根据以上不完整的统计图提供的信息,解答下列问题:
(1)小张同学共调查了 名居民的年龄,扇形统计图中a= ;
(2)补全条形统计图,并注明人数;
(3)若在该辖区中随机抽取一人,那么这个人年龄是60岁及以上的概率为 ;
(4)若该辖区年龄在0~14岁的居民约有2400人,请估计该辖区居民有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段CD在线段AB上,且CD=2,若线段AB的长度是一个正整数,则图中以A,B,C,D这四点中任意两点为端点的所有线段长度之和可能是( )
![]()
A.28 B.29 C.30 D.31
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学新建了一栋四层的教学楼,每层楼有10间教室,进出这栋教学楼共有4个门,其中两个正门大小相同,两个侧门大小也相同.安全检查中,对4个门进行了测试,当同时开启一个正门和两个侧门时,2分钟内可以通过560名学生;当同时开启一个正门和一个侧门时,4分钟内可以通过800名学生.
(1)求平均每分钟一个正门和一个侧门各可以通过多少名学生?
(2)检查中发现,出现紧急情况时,因学生拥挤,出门的效率将降低20%,安全检查规定:在紧急情况下全楼的学生应在5分钟内通过这4个门安全撤离,假设这栋教学大楼每间教室最多有45名学生,问:该教学楼建造的这4个门是否符合安全规定?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
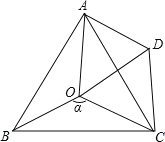
【题目】如图,点 O 是等边△ABC 内一点,∠AOB=105°,∠BOC 等于α,将△BOC 绕点 C 按 顺时针方向旋转 60°得△ADC,连接 OD.
(1)求证:△COD 是等边三角形.
(2)求∠OAD 的度数.
(3)探究:当α为多少度时,△AOD 是等腰三角形?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com