
 ,PB=4.
,PB=4.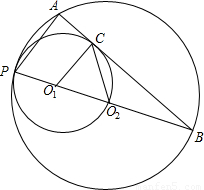
 ,PB=4,
,PB=4,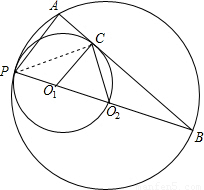
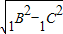 =
=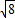 ,
,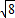 =tanBPC=tanBCO2,
=tanBPC=tanBCO2, .
.

 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案科目:初中数学 来源:2005年全国中考数学试题汇编《二次函数》(07)(解析版) 题型:解答题
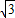 的等边三角形,其中O是坐标原点,顶点B在y轴的正半轴上.将△OAB折叠,使点A与OB边上的点P重合,折痕与OA、AB的交点分别是E、F.如果PE∥x轴,
的等边三角形,其中O是坐标原点,顶点B在y轴的正半轴上.将△OAB折叠,使点A与OB边上的点P重合,折痕与OA、AB的交点分别是E、F.如果PE∥x轴, x2+bx+c经过点P、E,求抛物线的解析式.
x2+bx+c经过点P、E,求抛物线的解析式.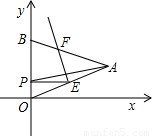
查看答案和解析>>
科目:初中数学 来源:2005年山东省日照市中考数学试卷(解析版) 题型:解答题
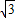 的等边三角形,其中O是坐标原点,顶点B在y轴的正半轴上.将△OAB折叠,使点A与OB边上的点P重合,折痕与OA、AB的交点分别是E、F.如果PE∥x轴,
的等边三角形,其中O是坐标原点,顶点B在y轴的正半轴上.将△OAB折叠,使点A与OB边上的点P重合,折痕与OA、AB的交点分别是E、F.如果PE∥x轴, x2+bx+c经过点P、E,求抛物线的解析式.
x2+bx+c经过点P、E,求抛物线的解析式.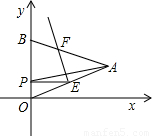
查看答案和解析>>
科目:初中数学 来源:2005年全国中考数学试题汇编《圆》(16)(解析版) 题型:解答题
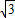 cm/s的速度向点A运动,⊙O1半径为2cm,⊙O2的半径为4cm,若O1、O2分别从点A、点B同时出发,运动的时间为t.
cm/s的速度向点A运动,⊙O1半径为2cm,⊙O2的半径为4cm,若O1、O2分别从点A、点B同时出发,运动的时间为t.
查看答案和解析>>
科目:初中数学 来源:2005年全国中考数学试题汇编《四边形》(10)(解析版) 题型:解答题
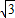 cm/s的速度向点A运动,⊙O1半径为2cm,⊙O2的半径为4cm,若O1、O2分别从点A、点B同时出发,运动的时间为t.
cm/s的速度向点A运动,⊙O1半径为2cm,⊙O2的半径为4cm,若O1、O2分别从点A、点B同时出发,运动的时间为t.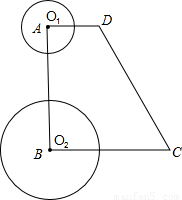
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com