
 如图,⊙O与⊙O′相交,AB为公共弦,圆心距⊙OO′=5cm,⊙O与⊙O′的半径分别为4cm和3cm,则AB的长为
如图,⊙O与⊙O′相交,AB为公共弦,圆心距⊙OO′=5cm,⊙O与⊙O′的半径分别为4cm和3cm,则AB的长为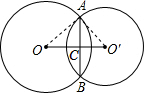 解:连接OA,O′A,设AB交OO′于点C,
解:连接OA,O′A,设AB交OO′于点C,| OA•O′A |
| OO′ |


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
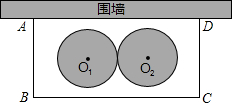 某学校要在围墙旁建一个长方形的中药材种植实习苗圃,苗圃的一边靠围墙(墙的长度不限),另三边用木栏围成,建成的苗圃为如图所示的长方形ABCD.已知木栏总长为120米,设AB边的长为x米,长方形ABCD的面积为S平方米.
某学校要在围墙旁建一个长方形的中药材种植实习苗圃,苗圃的一边靠围墙(墙的长度不限),另三边用木栏围成,建成的苗圃为如图所示的长方形ABCD.已知木栏总长为120米,设AB边的长为x米,长方形ABCD的面积为S平方米.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•茂名)如图,⊙O与直线l1相离,圆心O到直线l1的距离OB=2
(2012•茂名)如图,⊙O与直线l1相离,圆心O到直线l1的距离OB=2| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
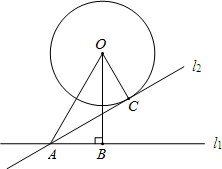 如图,⊙O与直线l1相离,圆心O到直线l1的距离OB=2
如图,⊙O与直线l1相离,圆心O到直线l1的距离OB=2 ,OA=4,将直线l1绕点A逆时针旋转30°后得到的直线l2刚好与⊙O相切于点C,则OC=________.
,OA=4,将直线l1绕点A逆时针旋转30°后得到的直线l2刚好与⊙O相切于点C,则OC=________.查看答案和解析>>
科目:初中数学 来源:2013年广东省湛江市中考数学模拟试卷(二)(解析版) 题型:填空题
 ,OA=4,将直线l1绕点A逆时针旋转30°后得到的直线l2刚好与⊙O相切于点C,则OC= .
,OA=4,将直线l1绕点A逆时针旋转30°后得到的直线l2刚好与⊙O相切于点C,则OC= .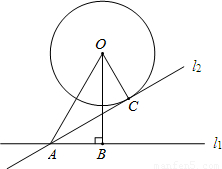
查看答案和解析>>
科目:初中数学 来源:2012年广东省茂名市中考数学试卷(解析版) 题型:填空题
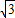 ,OA=4,将直线l1绕点A逆时针旋转30°后得到的直线l2刚好与⊙O相切于点C,则OC= .
,OA=4,将直线l1绕点A逆时针旋转30°后得到的直线l2刚好与⊙O相切于点C,则OC= .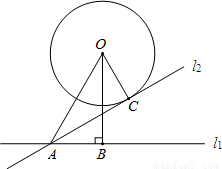
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com