
【题目】在数轴上,图中点A表示-36,点B表示44,动点P、Q分别从A、B两点同时出发,相向而行,动点P、Q的运动速度比之是3∶2(速度单位:1个单位长度/秒).12秒后,动点P到达原点O,动点Q到达点C,设运动的时间为t(t>0)秒.
(1)求OC的长;
(2)经过t秒钟,P、Q两点之间相距5个单位长度,求t的值;
(3)若动点P到达B点后,以原速度立即返回,当P点运动至原点时,动点Q是否到达A点,若到达,求提前到达了多少时间,若未能到达,说明理由.

【答案】(1)20;(2)t=15s或17s (3)![]() s.
s.
【解析】
(1)设P、Q速度分别为3m、2m,根据12秒后,动点P到达原点O列方程,求出P、Q的速度,由此即可得到结论.
(2)分两种情况讨论:①当A、B在相遇前且相距5个单位长度时;②当A、B在相遇后且相距5个单位长度时;列方程,求解即可.
(3)算出P运动到B再到原点时,所用的时间,再算出Q从B到A所需的时间,比较即可得出结论.
(1)设P、Q速度分别为3m、2m,根据题意得:12×3m=36,解得:m=1,∴P、Q速度分别为3、2,∴BC=12×2=24,∴OC=OB-BC=44-24=20.
(2)当A、B在相遇前且相距5个单位长度时:3t+2t+5=44+36,5t=75,∴ t=15(s);
当A、B在相遇后且相距5个单位长度时:3t+2t-5=44+36,5t=85,∴ t=17(s).
综上所述:t=15s或17s.
(3)P运动到原点时,t=![]() =
=![]() s,此时QB=2×
s,此时QB=2×![]() =
=![]() >44+38=80,∴Q点已到达A点,∴Q点已到达A点的时间为:
>44+38=80,∴Q点已到达A点,∴Q点已到达A点的时间为:![]() (s),故提前的时间为:
(s),故提前的时间为:![]() -40=
-40=![]() (s).
(s).


科目:初中数学 来源: 题型:
【题目】阅读下列材料.
让我们规定一种运算![]()
![]() =ad-cb,如
=ad-cb,如![]()
![]() =2×5-3×4=-2,再如
=2×5-3×4=-2,再如![]()
![]() =4x-2.按照这种运算规定,请解答下列问题.
=4x-2.按照这种运算规定,请解答下列问题.
(1)计算:![]()
![]() ;
;![]()
![]() ;
;![]()
![]() 的值;
的值;
(2)当x=-1时,求![]()
![]() 的值(要求写出计算过程).
的值(要求写出计算过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一墙墩(用线段AB表示)的影子是BC,小明(用线段DE表示)的影子是EF,在M处有一颗大树,它的影子是MN.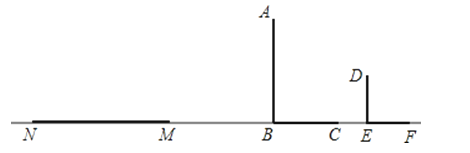
(1)试判断是路灯还是太阳光产生的影子,如果是路灯产生的影子确定路灯的位置(用点P表示).如果是太阳光请画出光线.
(2)在图中画出表示大树高的线段.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,为减少空气污染,北京市一些农村地区实施了煤改气工程,某燃气公司要从燃气站点A向B,C两村铺设天然气管道,经测量得知燃气站点A到B村距离约3千米,到 C村距离约4千米,B,C两村间距离约5千米.下面是施工部门设计的三种铺设管道方案示意图.请你通过计算说明在不考虑其它因素的情况下,下面哪个方案所用管道最短.
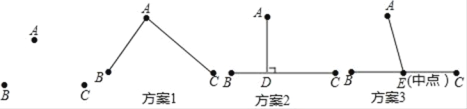
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,由一个边长为a的小正方形与两个长、宽分别为a,b的小长方形拼接成大长方形ABCD,则整个图形可表达出一些有关多项式因式分解的等式,请你写出其中任意三个等式:__________________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读并填空
问题:在一条直线上有A,B,C,D四个点,那么这条直线上总共有多少条线段?要解决这个问题,我们可以这样考虑,以A为端点的线段有AB,AC,AD 3条,同样以B为端点,以C为端点,以D为端点的线段也各有3条,这样共有4个3,即4×3=12(条),但AB和BA是同一条线段,即每一条线段重复一次,所以一共![]() 条线段. 那么,如果在一条直线上有5个点,则这条直线上共有_____________条线段. 如果在一条直线线上有n个点,那么这条直线上共有______________条线段.
条线段. 那么,如果在一条直线上有5个点,则这条直线上共有_____________条线段. 如果在一条直线线上有n个点,那么这条直线上共有______________条线段.
知识迁移:
如果在一个锐角∠AOB内部画2条射线OC,OD,那么这个图形中总共有____________个角,若在∠AOB内画n 条射线,则总共有___________个角.
学以致用:一段铁路上共有5个火车端,若一列客车往返过程中,必须停靠每个车站,则铁路局需为这段线路准备___________种不同的车票。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com