
知识背景:同学们已经学过有理数的大小比较,那么两个代数式如何比较大小呢?我们通常用作差法比较代数式大小。例如:已知M=2x+3,N=2x+1,比较M和N的大小。先求M-N,若M-N>0,则M>N;若M-N<0,则M<N;若M-N=0,则M=N,本题中因为M-N=2>0,所以M>N。
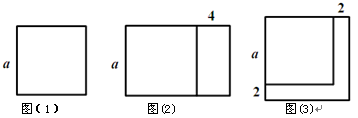
知识应用:图⑴是边长为a的正方形,将正方形一边不变,另一边增加4,得到如图⑵所示的新长方形,此长方形的面积为 ;将图(1)中正方形边长增加2得到如图⑶所示的新正方形,此正方形的面积为
;将图(1)中正方形边长增加2得到如图⑶所示的新正方形,此正方形的面积为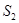

①用含a的代数式表示 ,
,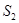 (需要化简)
(需要化简)
②请你用作差法比较 与
与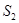 大小
大小
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2012-2013学年江苏省兴化市安丰中学七年级下学期第二次月考数学卷(带解析) 题型:解答题
知识背景:同学们已经学过有理数的大小比较,那么两个代数式如何比较大小呢?我们通常用作差法比较代数式大小。例如:已知M=2x+3,N=2x+1,比较M和N的大小。先求M-N,若M-N>0,则M>N;若M-N<0,则M<N;若M-N=0,则M=N,本题中因为M-N=2>0,所以M>N。
知识应用:图⑴是边长为a的正方形,将正方形一边不变,另一边增加4,得到如图⑵所示的新长方形,此长方形的面积为 ;将图(1)中正方形边长增加2得到如图⑶所示的新正方形,此正方形的面积为
;将图(1)中正方形边长增加2得到如图⑶所示的新正方形,此正方形的面积为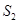
①用含a的代数式表示 ,
,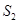 (需要化简)
(需要化简)
②请你用作差法比较 与
与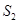 大小
大小
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:
知识背景:同学们已经学过有理数的大小比较,那么两个代数式如何比较大小呢?我们通常用作差法比较代数式大小。例如:已知M=2x+3,N=2x+1,比较M和N的大小。先求M-N,若M-N>0,则M>N;若M-N<0,则M<N;若M-N=0,则M=N,本题中因为M-N=2>0,所以M>N。
知识应用:图⑴是边长为a的正方形,将正方形一边![]() 不变,另一边增加4,得到如图⑵所示的新长方形,此长方形的面积为
不变,另一边增加4,得到如图⑵所示的新长方形,此长方形的面积为![]() ;将图(1)中正方形边长增加2得到如图⑶所示的新正方形,此正方形的面积为
;将图(1)中正方形边长增加2得到如图⑶所示的新正方形,此正方形的面积为![]()
①用含a的代数式表示![]() ,
,![]() (需要化简)
(需要化简)
 ②请你用作差法比较
②请你用作差法比较![]() 与
与![]() 大小
大小
图(1) 图(2) 图(3)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com