
分析 (1)把-$\overrightarrow{CB}$写成$\overrightarrow{BC}$,再根据平行四边形法则求解,然后利用勾股定理求出|$\overrightarrow{AC}$|即可;
(2)先表示出-$\overrightarrow{BC}$+$\overrightarrow{AC}$=$\overrightarrow{AB}$,然后求解即可;
(3)根据(1)的计算方法求解即可;
(4)根据平行四边形法则表示出$\overrightarrow{AC}$、$\overrightarrow{BD}$,然后整理即可得解.
解答 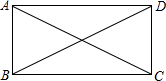 解:(1)∵-$\overrightarrow{CB}$=$\overrightarrow{BC}$,
解:(1)∵-$\overrightarrow{CB}$=$\overrightarrow{BC}$,
∴|$\overrightarrow{AB}$-$\overrightarrow{CB}$|=|$\overrightarrow{AB}$+$\overrightarrow{BC}$|=|$\overrightarrow{AC}$|,
∵四边形ABCD是矩形,且AB=1,BC=2,
∴AC=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,
∴|$\overrightarrow{AB}$-$\overrightarrow{CB}$|=$\sqrt{5}$;
(2)∵-$\overrightarrow{BC}$+$\overrightarrow{AC}$=$\overrightarrow{AC}$-$\overrightarrow{BC}$=$\overrightarrow{AB}$,
∴|$\overrightarrow{AB}$-$\overrightarrow{BC}$+$\overrightarrow{AC}$|=|$\overrightarrow{AB}$+$\overrightarrow{AB}$|=2|$\overrightarrow{AB}$|,
∵AB=1,
∴|$\overrightarrow{AB}$-$\overrightarrow{BC}$+$\overrightarrow{AC}$|=2;
(3)由(1)可知,$\overrightarrow{AB}$-$\overrightarrow{CB}$-$\overrightarrow{AC}$=$\overrightarrow{AC}$-$\overrightarrow{AC}$=0;
(4)由平行四边形法则得,$\overrightarrow{AC}$=$\overrightarrow{AB}$+$\overrightarrow{BC}$,
$\overrightarrow{BD}$=$\overrightarrow{BA}$+$\overrightarrow{BC}$,
所以,$\overrightarrow{AC}$+$\overrightarrow{BD}$-$\overrightarrow{BC}$=$\overrightarrow{AB}$+$\overrightarrow{BC}$+$\overrightarrow{BA}$+$\overrightarrow{BC}$-$\overrightarrow{BC}$=$\overrightarrow{BC}$.
点评 本题考查了平面向量,向量的问题,熟练掌握平行四边形法则和三角形法则是解题的关键,本题要注意互为相反向量的应用.


 步步高达标卷系列答案
步步高达标卷系列答案科目:初中数学 来源: 题型:解答题
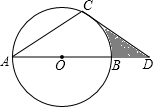 如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠D=30°.
如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠D=30°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图所示,在平面直角坐标系中,半径均为1个单位长度的半圆O1,O2,O3,…组成一条平滑的曲线.点P从原点O出发,沿这条曲线向右运动,速度为每秒$\frac{π}{2}$个单位长度,则第15秒时,点P的坐标是( )
如图所示,在平面直角坐标系中,半径均为1个单位长度的半圆O1,O2,O3,…组成一条平滑的曲线.点P从原点O出发,沿这条曲线向右运动,速度为每秒$\frac{π}{2}$个单位长度,则第15秒时,点P的坐标是( )| A. | (15,1) | B. | (15,-1) | C. | (30,1) | D. | (30,-1) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
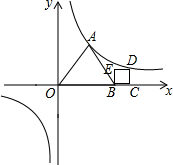 已知,反比例函数y=$\frac{\sqrt{3}}{x}$的图象上有两点A和D,且△OBA是等边三角形,四边形BCDE是正方形,则D点坐标(1+$\sqrt{\sqrt{3}+1}$,-1+$\sqrt{\sqrt{3}+1}$).
已知,反比例函数y=$\frac{\sqrt{3}}{x}$的图象上有两点A和D,且△OBA是等边三角形,四边形BCDE是正方形,则D点坐标(1+$\sqrt{\sqrt{3}+1}$,-1+$\sqrt{\sqrt{3}+1}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 一艘船在小岛A的南偏西37°方向的B处,AB=20海里,船自西向东航行1.5小时后到达C处,测得小岛A在点C的北偏西50°方向,求该船航行的速度(精确到0.1海里/小时?)
一艘船在小岛A的南偏西37°方向的B处,AB=20海里,船自西向东航行1.5小时后到达C处,测得小岛A在点C的北偏西50°方向,求该船航行的速度(精确到0.1海里/小时?)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
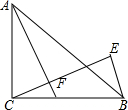 如图,△ABC中,∠ACB=90°,AC=BC,D为BC的中点,CF⊥AD于F,BE⊥CF交CF的延长线于E,求$\frac{BE}{AF}$的值.
如图,△ABC中,∠ACB=90°,AC=BC,D为BC的中点,CF⊥AD于F,BE⊥CF交CF的延长线于E,求$\frac{BE}{AF}$的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com