
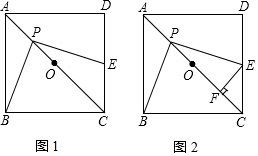
分析 (1)作辅助线,构建全等三角形,根据ASA证明△BMP≌△PNE可得结论;
(2)如图2,连接OB,通过证明△OBP≌△FPE,得PF=OB,则PF为定值是$\sqrt{2}$.
解答 解:(1)证明:
如图1,过P作MN∥AD,交AB于M,交CD于N,
∵PB⊥PE,
∴∠BPE=90°,
∴∠MPB+∠EPN=90°,
∵四边形ABCD是正方形,
∴∠BAD=∠D=90°,
∵AD∥MN,
∴∠BMP=∠BAD=∠PNE=∠D=90°,
∴∠MPB+∠MBP=90°,
∴∠EPN=∠MBP,
Rt△PNC中,∠PCN=45°,
∴△PNC是等腰直角三角形,
∴PN=CN,
∵∠BMP=∠PNC=∠ABC=90°,
∴四边形MBCN是矩形,
∴BM=CN,
∴BM=PN,
∴△BMP≌△PNE(ASA),
∴PB=PE;
(2)在P点运动的过程中,PF的长度不发生变化,理由是:
如图2,连接OB,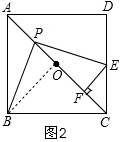
∵点O是正方形ABCD对角线AC的中点,
∴OB⊥AC,
∴∠AOB=90°,
∴∠AOB=∠EFP=90°,
∴∠OBP+∠BPO=90°,
∵∠BPE=90°,
∴∠BPO+∠OPE=90°,
∴∠OBP=∠OPE,
由(1)得:PB=PE,
∴△OBP≌△FPE,
∴PF=OB,
∵AB=2,△ABO是等腰直角三角形,
∴OB=$\frac{2}{\sqrt{2}}$=$\sqrt{2}$,
∴PF为定值是$\sqrt{2}$.
点评 本题是一个动态几何题,考查用正方形性质、等腰直角三角形的性质、三角形全等的条件和性质进行有条理的思考和表达能力.利用条件构造三角形全等是解题的关键.本题涉及知识点较多,综合性很强,难度适中.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
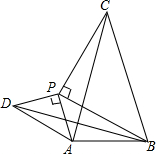 如图,已知线段AB=2,点P是线段AB外的一个动点,且PA=1,以PA,PB为腰向外作等腰直角三角形PAD和等腰直角三角形PBC,连结AC,BD.
如图,已知线段AB=2,点P是线段AB外的一个动点,且PA=1,以PA,PB为腰向外作等腰直角三角形PAD和等腰直角三角形PBC,连结AC,BD.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
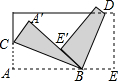 将一长方形纸片,按图中的方式折叠,BC、BD为折痕,折叠后点E′刚好落在A′B上,则∠CBD的度数为( )
将一长方形纸片,按图中的方式折叠,BC、BD为折痕,折叠后点E′刚好落在A′B上,则∠CBD的度数为( )| A. | 60° | B. | 75° | C. | 90° | D. | 95° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
| 摸到白球的次数m | 65 | 124 | 178 | 302 | 481 | 599 | 1803 |
| 摸到白球的频率$\frac{m}{n}$ | 0.65 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
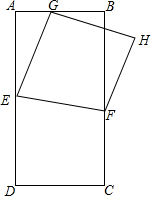 矩形ABCD满足BC=2AB,E、F分别为AD、BC边上的动点,连接EF,沿EF将四边形DEFC翻折至四边形GEFH,点G落在AB上.
矩形ABCD满足BC=2AB,E、F分别为AD、BC边上的动点,连接EF,沿EF将四边形DEFC翻折至四边形GEFH,点G落在AB上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com