
【题目】如图,点![]() 是
是![]() 直径
直径![]() 上的一点,过
上的一点,过![]() 作直线
作直线![]() ,分别交
,分别交![]() 于
于![]() ,
,![]() 两点,连接
两点,连接![]() ,并将线段
,并将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,连接
,连接![]() ,分别交
,分别交![]() 和
和![]() 于
于![]() ,
,![]() ,连接
,连接![]() .
.
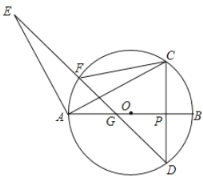
(Ⅰ)求证:![]() ;
;
(Ⅱ)若点![]() 在直径
在直径![]() 上运动(不与点
上运动(不与点![]() ,
,![]() 重合),其它条件不变,请问
重合),其它条件不变,请问![]() 是否为定值?若是,请求出其值;若不是,请说明理由.
是否为定值?若是,请求出其值;若不是,请说明理由.
【答案】(Ⅰ)见解析;(Ⅱ)是定值![]() ,理由见解析;
,理由见解析;
【解析】
(Ⅰ)连接AD,由同弧所对的圆周角相等可知∠ACF=∠ADF,由旋转的性质可知AC=AE,利用垂径定理证得AD=AC,推出AE=AD,∠AED=∠ADF,即可推出结论;
(Ⅱ)过点E作EN∥CD,过点D作DN⊥CD,且EN与直线AB交于点M,与直线DN交于点N,先证四边形MNDP是矩形,△EAM≌△ACP,推出MN=PD,MP=ND,EM=AP,AM=CP,再证明△END为等腰直角三角形,推出△EMG为等腰直角三角形,即可通过锐角三角函数推出结论.
解:(Ⅰ)连接![]() ,由同弧所对的圆周角相等可知∠ACF=∠ADF,
,由同弧所对的圆周角相等可知∠ACF=∠ADF,

∵AE是由线段AC绕点A逆时针旋转90°得到,
∴AC=AE,
∵CD⊥AB,
∴AB垂直平分CD,
∴AC=AD,
∴AE=AD,
∴∠AED=∠ADF,
∴∠ACF=∠AED;
(Ⅱ)是定值![]() ,
,
理由:过点E作EN∥CD,过点D作DN⊥CD,且EN与直线AB交于点M,与直线DN交于点N,
∵∠EAC=∠CPA=90°,
∴∠EAM+∠CAB=∠CAB+∠ACP=90°,
∴∠EAM=∠ACP,
∵DN⊥CD,CD⊥AB,
∴DN∥AB,
又∵EN∥CD,
∴四边形MNDP是矩形,
∴∠AME=∠APC=90°,
∵AC=AE,∠EAM=∠ACP,∠AME=∠APC,
∴△EAM≌△ACP,
∴EM=AP,AM=CP,
∵四边形MNDP是矩形,
∴MN=PD,MP=ND,
∵AB是直径,CD⊥AB,
∴MN=PD=CP=AM,
又∵EM=AP,
∴EM+MN=AP+AM,即EN=MP=ND,
∴△END是等腰直角三角形,
∴∠EDN=45°,
∵DN∥AB,
∴∠EGM=∠EDN=45°,
∴△EMG是等腰直角三角形,
∴![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】 如图,平面直角坐标系中,矩形OABC的顶点B的坐标为(7,5),顶点A,C分别在x轴,y轴上,点D的坐标为(0,1),过点D的直线与矩形OABC的边BC交于点G,且点G不与点C重合,以DG为一边作菱形DEFG,点E在矩形OABC的边OA上,设直线DG的函数表达式为y=kx+b
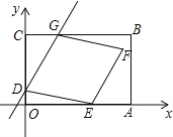
(1)当CG=OD时,求直线DG的函数表达式;
(2)当点E的坐标为(5,0)时,求直线DG的函数表达式;
(3)连接BF,设△FBG的面积为S,CG的长为a,请直接写出S与a的函数表达式及自变量a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知m,n分别是关于x的一元二次方程ax2+bx+c=a与ax2+bx+c=b的一个根,且m=n+1.
(1)当m=2,a=﹣1时,求b与c的值;
(2)用只含字母a,n的代数式表示b;
(3)当a<0时,函数y=ax2+bx+c满足b2﹣4ac=a,b+c≥2a,n≤﹣![]() ,求a的取值范围.
,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
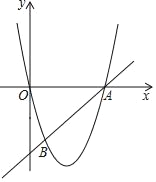
【题目】如图,在平面直角坐标系xOy中,直线AB与抛物线y=ax2+bx交于点A(6,0)和点B(1,﹣5).
(1)求这条抛物线的表达式和直线AB的表达式;
(2)如果点C在直线AB上,且∠BOC的正切值是![]() ,求点C的坐标.
,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
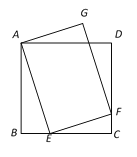
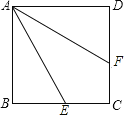
【题目】如图,已知正方形ABCD中,点E是BC上的一个动点,EF⊥AE交CD于点F,以AE,EF为边作矩形AEFG,若AB=4,则点G到AD距离的最大值是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,点E、F分别在线段BC、DC上,线段AE绕点A逆时针旋转后与线段AF重合.若![]() ,则旋转的角度是( )
,则旋转的角度是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】截至北京时间2020年3月22日14时30分,全球新冠肺炎确诊病例达305740例,超过30万,死亡病例累计12762人,将“305740”这个数字用科学记数法表示保留两位有效数字为( )
A.3.05740×105B.3.05×105C.3.0×105D.3.1×105
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在半圆O中,AB为直径,AC、AD为两条弦,且∠CAD+∠CAB=90°.
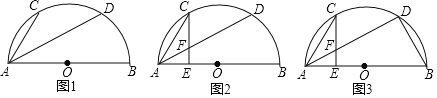
(1)如图1,求证:弧AC等于弧CD;
(2)如图2,点E在直径AB上,CE交AD于点F,若AF=CF,求证:AD=2CE;
(3)如图3,在(2)的条件下,连接BD,若AE=4,BD=12,求弦AC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com