
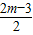 =0.
=0. <m<6,试判断方程两个实数根的符号,并证明你的结论.
<m<6,试判断方程两个实数根的符号,并证明你的结论.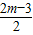 =-2m+12,
=-2m+12,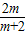 ,α•β=
,α•β=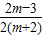 ,
, <m<6,则-
<m<6,则-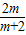 <0,
<0,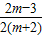 >0;
>0;

 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源:2002年全国中考数学试题汇编《二次函数》(04)(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2002年广东省湛江市中考数学试卷(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2002年全国中考数学试题汇编《一元二次方程》(04)(解析版) 题型:解答题
 =0.
=0. <m<6,试判断方程两个实数根的符号,并证明你的结论.
<m<6,试判断方程两个实数根的符号,并证明你的结论.查看答案和解析>>
科目:初中数学 来源:2002年广东省湛江市中考数学试卷(解析版) 题型:解答题
 上运动,其他条件不变,问应再具备什么条件可使结论BG2=BF•BO成立?(要求画出示意图并说明理由)
上运动,其他条件不变,问应再具备什么条件可使结论BG2=BF•BO成立?(要求画出示意图并说明理由)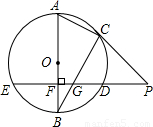
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com