练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    2．某超市为了测定某个时间段收银台开放方案，统计了这个时间段本超市顾客在收银台排队付款的等待时间，并绘制成如下的频数分布直方图（图中等待时间2分钟到3分钟表示大于或等于2分钟而小于3分钟，其它类同）．这个时间段内顾客等待时间不少于6分钟的人数为7．

    分析 根据题意和频数分布直方图可以得到这个时间段内顾客等待时间不少于6分钟的人数，本题得以解决．

    解答 解：由频数分布直方图可得，
    这个时间段内顾客等待时间不少于6分钟的人数为：5+2=7，
    故答案为：7．

    点评 本题考查频数分布直方图，解题的关键是明确题意，利用数形结合的思想解答问题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    12．一组数如下，9.0、9.0、9.2、9.8、8.8、9.2、9.5、9.2，这组数据的中位数是9.2，众数是9.2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．计算：
    （1）$\frac{1}{a-2}$-$\frac{1}{a+2}$-$\frac{1}{{a}^{2}-4}$
    （2）（$\frac{3a}{a+2}$-$\frac{a}{a-2}$）÷$\frac{2a}{{a}^{2}-4}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．计算：（x+y）（x-y）-x（x+y）+2xy．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．下列根式中，与$\sqrt{2}$是同类二次根式的是（　　）
    A．$\sqrt{24}$B．$\sqrt{20}$C．$\sqrt{\frac{3}{2}}$D．$\sqrt{18}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    7．如图，在△ABC中，AB=AC=6，AB的垂直平分线交AB于点E，交BC于点D，连接AD，若AD=4，则DC=5．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

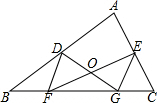    14．如图，在△ABC中D，E分别是AB，AC的中点，点F，G在BC上，且BC=4BF=4CG，EF与DG相交于点O，若∠DFE=40°，∠DGE=80°，那么∠DOE的度数是（　　）
    A．100°B．120°C．140°D．160°

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    11．下列说法：
    ①一组对边平行，另一组对边相等的四边形是平行四边形；
    ②两条对角线相等且互相平分的四边形是矩形；
    ③在反比例函数y=$\frac{4}{x}$中，如果自变量x＜2时，那么函数值y＞2．
    其中正确的有（　　）
    A．0个B．1个C．2个D．3个

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．如图，矩形OABC的两边OA，OC分别在x轴和y轴的正半轴上，点B的坐标为（4$\sqrt{3}$，4），点D在CB上，且CD：DB=2：1，OB交AD于点E．平行于x轴的直线l从原点O出发，以每秒1个单位长度的速度沿y轴向上平移，到C点时停止；l与线段OB，AD分别相交与M，N两点，以MN为边作等边△MNP（点P在线段MN的下方）．设直线l的运动时间为t（秒），△MNP与△OAB重叠部分的面积为S（平分单位）．
    （1）直接写出点E的坐标；
    （2）求S与t的函数关系式；
    （3）是否存在某一时刻t，使得S=$\frac{1}{2}$S△ABD成立？若存在，请求出此时t的值；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案