
【题目】在平面直角坐标系中,O为原点,点A(﹣2,0),点B(0,2),点E,点F分别为OA,OB的中点.若正方形OEDF绕点O顺时针旋转,得正方形OE′D′F′,记旋转角为α. 
(1)如图①,当α=90°时,求AE′,BF′的长;
(2)如图②,当α=135°时,求证AE′=BF′,且AE′⊥BF′;
【答案】
(1)解:当α=90°时,点E′与点F重合,如图①.
∵点A(﹣2,0)点B(0,2),
∴OA=OB=2.
∵点E,点F分别为OA,OB的中点,
∴OE=OF=1
∵正方形OE′D′F′是正方形OEDF绕点O顺时针旋转90°得到的,
∴OE′=OE=1,OF′=OF=1.
在Rt△AE′O中,
AE′= ![]() .
.
在Rt△BOF′中,
BF′= ![]() .
.
∴AE′,BF′的长都等于 ![]() .
.

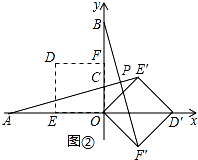
(2)解:当α=135°时,如图②.
∵正方形OE′D′F′是由正方形OEDF绕点O顺时针旋转135°所得,
∴∠AOE′=∠BOF′=135°.
在△AOE′和△BOF′中,
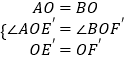 ,
,
∴△AOE′≌△BOF′(SAS).
∴AE′=BF′,且∠OAE′=∠OBF′.
∵∠ACB=∠CAO+∠AOC=∠CBP+∠CPB,∠CAO=∠CBP,
∴∠CPB=∠AOC=90°
∴AE′⊥BF′.
(Ⅲ)若直线AE′与直线BF′相交于点P,求点P的纵坐标的最大值(直接写出结果即可).
解:∵∠BPA=∠BOA=90°,∴点P、B、A、O四点共圆,
∴当点P在劣弧OB上运动时,点P的纵坐标随着∠PAO的增大而增大.
∵OE′=1,∴点E′在以点O为圆心,1为半径的圆O上运动,
∴当AP与⊙O相切时,∠E′AO(即∠PAO)最大,
此时∠AE′O=90°,点D′与点P重合,点P的纵坐标达到最大.
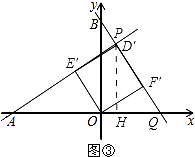
过点P作PH⊥x轴,垂足为H,如图③所示.
∵∠AE′O=90°,E′O=1,AO=2,
∴∠E′AO=30°,AE′= ![]() .
.
∴AP= ![]() +1.
+1.
∵∠AHP=90°,∠PAH=30°,
∴PH= ![]() AP=
AP= ![]() .
.
∴点P的纵坐标的最大值为 ![]() .
.
【解析】(1)利用勾股定理即可求出AE′,BF′的长.(2)运用全等三角形的判定与性质、三角形的外角性质就可解决问题.(3)首先找到使点P的纵坐标最大时点P的位置(点P与点D′重合时),然后运用勾股定理及30°角所对的直角边等于斜边的一半等知识即可求出点P的纵坐标的最大值.
【考点精析】掌握三角形的外角和含30度角的直角三角形是解答本题的根本,需要知道三角形一边与另一边的延长线组成的角,叫三角形的外角;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】杭州国际动漫节开幕前,某动漫公司预测某种动漫玩具能够畅销,就用32000元购进了一批这种玩具,上市后很快脱销,动漫公司又用68000元购进第二批这种玩具,所购数量是第一批购进数量的2倍,但每套进价多了10元.
(1)该动漫公司两次共购进这种玩具多少套?
(2)如果这两批玩具每套的售价相同,且全部售完后总利润率不低于20%,那么每套售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
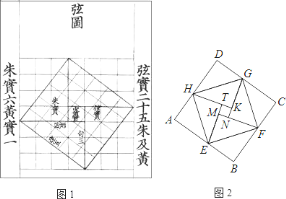
【题目】汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”(如图![]() ).图
).图![]() 是由弦图变化得到的,它由八个全等的直角三角形拼接而成,记图中正方形
是由弦图变化得到的,它由八个全等的直角三角形拼接而成,记图中正方形![]() 、正方形
、正方形![]() 、正方形
、正方形![]() 的面积分别为
的面积分别为![]() 、
、![]() 、
、![]() .若
.若![]() ,则
,则![]() 的值是( )
的值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2) 如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=![]() ,其中
,其中![]() 为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】考试前,同学们总会采用各种方式缓解考试压力,以最佳状态迎接考试.某校对该校九年级的部分同学做了一次内容为“最适合自己的考前减压方式”的调查活动,学校将减压方式分为五类,同学们可根据自己的情况必选且只选其中一类.学校收集整理数据后,绘制了图1和图2两幅不完整的统计图,请根据统计图中信息解答下列问题: 
(1)这次抽样调查中,一共抽查了多少名学生?
(2)请补全条形统计图;
(3)请计算扇形统计图中“享受美食”所对应扇形的圆心角的度数;
(4)根据调查结果,估计该校九年级500名学生中采用“听音乐”来减压方式的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知函数![]() 的图象与x轴、y轴分别交于点A,B,与函数y=x的图象交于点M,点M的横坐标为2.在x轴上有一点P (a,0)(其中a>2),过点P作x轴的垂线,分别交函数
的图象与x轴、y轴分别交于点A,B,与函数y=x的图象交于点M,点M的横坐标为2.在x轴上有一点P (a,0)(其中a>2),过点P作x轴的垂线,分别交函数![]() 和y=x的图象于点C,D.
和y=x的图象于点C,D.
(1)求点A的坐标;
(2)若OB=CD,求a的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的两点OA、OC分别在x轴、y轴的正半轴上,点G为矩形对角线的交点,经过点G的双曲线y= ![]() 在第一象限的图象与BC相交于点M,交AB于N,若已知S△MBN=9,则k的值为 .
在第一象限的图象与BC相交于点M,交AB于N,若已知S△MBN=9,则k的值为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,△OAB如图放置,点A的坐标为(3,4),点P是AB边上的一点,过点P的反比例函数 ![]() 与OA边交于点E,连接OP.
与OA边交于点E,连接OP.
(1)如图1,若点B的坐标为(5,0),且△OPB的面积为 ![]() ,求反比例函数的解析式;
,求反比例函数的解析式;
(2)如图2,过P作PC∥OA,与OB交于点C,若 ![]() ,并且△OPC的面积为
,并且△OPC的面积为 ![]() ,求OE的长.
,求OE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com