
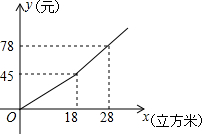
 我国很多城市水资源缺乏,为了增强居民的节水意识,某市制定了每月用水18立方米以内(不含18立方米)和用水18立方米及以上两种收费标准(收费标准指每立方米水的价格),某用户每月应交水费y(元)是用水量x(立方米)的函数,其函数图象如图所示.
我国很多城市水资源缺乏,为了增强居民的节水意识,某市制定了每月用水18立方米以内(不含18立方米)和用水18立方米及以上两种收费标准(收费标准指每立方米水的价格),某用户每月应交水费y(元)是用水量x(立方米)的函数,其函数图象如图所示.| 用水量/立方米 | 水费/元 | |
| 小刚 | 15 | 37.5 |
| 小丽 | 25 | 68.1 |
分析 (1)根据图象利用待定系数法分0≤x<18和x≥18两种情形,分别求解即可.
(2)利用(1)的结论计算即可.
(3)根据条件列出不等式即可解决问题.
解答 解:(1)当0≤x<18时,设y=kx,
由题意45=18k,解得k=2.5.
∴y=2.5x.
当x≥18时,设y=k′x+b,由题意$\left\{\begin{array}{l}{18k′+b=45}\\{28k′+b=78}\end{array}\right.$,解得$\left\{\begin{array}{l}{k′=3.3}\\{b=14.4}\end{array}\right.$
∴y=3.3x-14.4.
(2)x=15时,y=2.5×15=37.5元,
x=25时,y=3.3×25-14.4=68.1元.
故答案分别为37.5,68.1.
(3)当y≤51.6时,3.3x-14.4≤56.1,
解得,x≤20,
所以这个月最多可用20立方米水.
点评 本题考查一次函数的应用,一元一次不等式等知识,解题的关键是学会待定系数法确定函数解析式,读懂图象信息,学会利用不等式解决实际问题,属于中考常考题型.


科目:初中数学 来源: 题型:选择题
| 甲 | 乙 | 丙 | 丁 | |
| $\overline{x}$ | 8.9 | 9.5 | 9.5 | 8.9 |
| s2 | 0.92 | 0.92 | 1.01 | 1.03 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
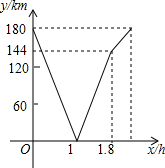 一辆货车从A地去B地,一辆轿车从B地去A地,同时出发,匀速行驶,各自到达终点后停止,轿车的速度大于货车的速度.两辆车之间的距离为y(km)与货车行驶的时间为x(h)之间的函数关系如图所示.
一辆货车从A地去B地,一辆轿车从B地去A地,同时出发,匀速行驶,各自到达终点后停止,轿车的速度大于货车的速度.两辆车之间的距离为y(km)与货车行驶的时间为x(h)之间的函数关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x=1 | B. | 5x=-1 | C. | x=3 | D. | 5x=3 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
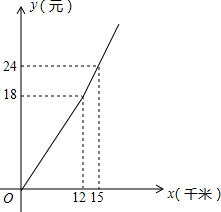 随着“互联网+”时代的到来,一种新型的打车方式受到大众欢迎.该打车方式采用阶梯收费标准.打车费用y(单位:元)与行驶里程x(单位:千米)的函数关系如图所示.如果小明某次打车行驶里程为20千米,则他的打车费用为( )
随着“互联网+”时代的到来,一种新型的打车方式受到大众欢迎.该打车方式采用阶梯收费标准.打车费用y(单位:元)与行驶里程x(单位:千米)的函数关系如图所示.如果小明某次打车行驶里程为20千米,则他的打车费用为( )| A. | 32元 | B. | 34元 | C. | 36元 | D. | 40元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com