练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    如图，在Rt△ABC中，∠ACB=90°，AB=10，cosB=
    4
    5
    ，CD⊥AB于点D，求CD的长．
    考点：解直角三角形
    专题：
    分析：先在Rt△ABC中，由余弦函数的定义得出cosB=
    BC
    AB
    =
    4
    5
    ，于是BC=
    4
    5
    AB=8．然后在Rt△BCD中，由余弦函数的定义得出cosB=
    BD
    BC
    =
    4
    5
    ，那么BD=
    4
    5
    BC=
    32
    5
    ，再利用勾股定理得到CD=
    		BC2-BD2
    =
    24
    5
    ．
    解答：解：∵在Rt△ABC中，∠ACB=90°，AB=10，cosB=
    BC
    AB
    =
    4
    5
    ，
    ∴BC=
    4
    5
    AB=8．
    ∵在Rt△BCD中，cosB=
    BD
    BC
    =
    4
    5
    ，
    ∴BD=
    4
    5
    BC=
    32
    5
    ，
    ∴CD=
    		BC2-BD2
    =
    24
    5
    ．
    点评：本题考查了解直角三角形，锐角三角函数的定义，勾股定理，求出BC的长是解题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

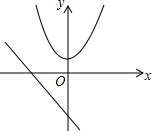    如图，坐标系中有抛物线c：y=x2+m和直线l：y=-2x-2．
    （1）求m取何值时，抛物线c与直线l没有公共点；
    （2）变化m，当抛物线c的顶点在直线l上时，求直线l被它截得的线段长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    抛物线y=2x2-x的顶点坐标是
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    某学校开展“文明礼仪”演讲比赛，八（1）、八（2）班派出的5名选手的比赛成绩如图所示：

    （1）根据图，完成表格：
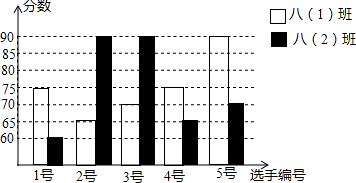
    平均数（分）中位数（分）极差（分）方差
    八（1）班75
     
    		25
     
    八（2）班7570
     
    		160
    （2）结合两班选手成绩的平均分和方差，分析两个班级参加比赛选手的成绩；
    （3）如果在每班参加比赛的选手中分别选出3人参加决赛，从平均分看，你认为哪个班的实力更强一些？并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，∠C=90°，以AC为半径的圆C与AB相交于点D．若AC=3，CB=4，求BD长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图所示，其中是轴对称图形的是（　　）
    A、
    B、
    C、
    D、

    查看答案和解析>>

    科目：初中数学 来源： 题型：

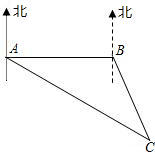    某客轮在C点失事后，海上搜救中心立即通知位于A、B两处的专业救助轮前往出事地点协助搜索．B在A的正东方向，且相距100海里，接到通知后，测得出事地点C在A的南偏东60°，C在B的南偏东30°．B处救助轮赶到出事地点C需要4小时，如果A，B两处救助轮航行速度相同，试问A处救助轮赶到出事地点C需要多长时间？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    用长为8米的铝合金制成如图所示的窗框，若设窗框的宽为x米，窗户的透光面积为S平方米，则S关于x的函数关系式为
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    计算：
    （1）(
    1
    3
    -
    5
    7
    -
    2
    5
    )×105
    （2）99
    17
    18
    ×9    ．

    查看答案和解析>>

    同步练习册答案