
”¾ĢāÄæ”æČēĶ¼£¬½«Ņ»ĢõŹżÖįŌŚŌµć![]() ŗĶµć
ŗĶµć![]() “¦ø÷ÕŪŅ»ĻĀ£¬µĆµ½Ņ»Ģõ”°ÕŪĻߏżÖį”±£¬Ķ¼ÖŠµć
“¦ø÷ÕŪŅ»ĻĀ£¬µĆµ½Ņ»Ģõ”°ÕŪĻߏżÖį”±£¬Ķ¼ÖŠµć![]() ±ķŹ¾-12£¬µć
±ķŹ¾-12£¬µć![]() ±ķŹ¾10£¬µć
±ķŹ¾10£¬µć![]() ±ķŹ¾20£¬ĪŅĆĒ³Ęµć
±ķŹ¾20£¬ĪŅĆĒ³Ęµć![]() ŗĶµć
ŗĶµć![]() ŌŚŹżÖįÉĻĻą¾ą32øö³¤¶Čµ„Ī»£®¶Æµć
ŌŚŹżÖįÉĻĻą¾ą32øö³¤¶Čµ„Ī»£®¶Æµć![]() “Óµć
“Óµć![]() ³ö·¢£¬ŅŌ2µ„Ī»/ĆėµÄĖŁ¶ČŃŲ×Å”°ÕŪĻߏżÖį”±µÄÕż·½ĻņŌĖ¶Æ£¬“Óµć
³ö·¢£¬ŅŌ2µ„Ī»/ĆėµÄĖŁ¶ČŃŲ×Å”°ÕŪĻߏżÖį”±µÄÕż·½ĻņŌĖ¶Æ£¬“Óµć![]() ŌĖ¶Æµ½µć
ŌĖ¶Æµ½µć![]() ĘŚ¼äĖŁ¶Č±äĪŖŌĄ“µÄŅ»°ė£¬Ö®ŗóĮ¢æĢ»Öø“ŌĖŁ£»Ķ¬Ź±£¬¶Æµć
ĘŚ¼äĖŁ¶Č±äĪŖŌĄ“µÄŅ»°ė£¬Ö®ŗóĮ¢æĢ»Öø“ŌĖŁ£»Ķ¬Ź±£¬¶Æµć![]() “Óµć
“Óµć![]() ³ö·¢£¬ŅŌ1µ„Ī»/ĆėµÄĖŁ¶ČŃŲ×ÅÕŪĻߏżÖįµÄøŗ·½ĻņŌĖ¶Æ£¬“Óµć
³ö·¢£¬ŅŌ1µ„Ī»/ĆėµÄĖŁ¶ČŃŲ×ÅÕŪĻߏżÖįµÄøŗ·½ĻņŌĖ¶Æ£¬“Óµć![]() ŌĖ¶Æµ½µć
ŌĖ¶Æµ½µć![]() ĘŚ¼äĖŁ¶Č±äĪŖŌĄ“µÄĮ½±¶£¬Ö®ŗóŅ²Į¢æĢ»Öø“ŌĖŁ£®ÉčŌĖ¶ÆµÄŹ±¼äĪŖ
ĘŚ¼äĖŁ¶Č±äĪŖŌĄ“µÄĮ½±¶£¬Ö®ŗóŅ²Į¢æĢ»Öø“ŌĖŁ£®ÉčŌĖ¶ÆµÄŹ±¼äĪŖ![]() Ćė£®Ōņ£ŗ
Ćė£®Ōņ£ŗ
£Ø1£©¶Æµć![]() “Óµć
“Óµć![]() ŌĖ¶ÆÖĮµć
ŌĖ¶ÆÖĮµć![]() ŠčŅŖŹ±¼ä¶ąÉŁĆė£æ
ŠčŅŖŹ±¼ä¶ąÉŁĆė£æ
£Ø2£©Čō![]() £¬
£¬![]() Į½µćŌŚµć
Į½µćŌŚµć![]() “¦ĻąÓö£¬Ōņµć
“¦ĻąÓö£¬Ōņµć![]() ŌŚÕŪĻߏżÖįÉĻĖł±ķŹ¾µÄŹżŹĒ¶ąÉŁ£æ
ŌŚÕŪĻߏżÖįÉĻĖł±ķŹ¾µÄŹżŹĒ¶ąÉŁ£æ
£Ø3£©Ēóµ±![]() ĪŖŗĪÖµŹ±£¬
ĪŖŗĪÖµŹ±£¬![]() ”¢
”¢![]() Į½µćŌŚŹżÖįÉĻĻą¾ąµÄ³¤¶ČÓė
Į½µćŌŚŹżÖįÉĻĻą¾ąµÄ³¤¶ČÓė![]() ”¢
”¢![]() Į½µćŌŚŹżÖįÉĻĻą¾ąµÄ³¤¶ČĻąµČ£®
Į½µćŌŚŹżÖįÉĻĻą¾ąµÄ³¤¶ČĻąµČ£®
”¾“š°ø”æ£Ø1£©21£»£Ø2£©6£»£Ø3£©µ±![]() Ź±£¬
Ź±£¬![]() £®
£®
”¾½āĪö”æ
£Ø1£©øł¾ŻĀ·³Ģ³żŅŌĖŁ¶ČµČÓŚŹ±¼ä£¬æɵƓš°ø£»
£Ø2£©øł¾ŻĻąÓöŹ±![]() £¬
£¬![]() Į½µćŌŚĻ߶Ī
Į½µćŌŚĻ߶Ī![]() ÉĻ£¬øł¾Ż
ÉĻ£¬øł¾Ż![]() =10£¬æɵƷ½³Ģ£¬øł¾Ż½ā·½³Ģ£¬æɵƓš°ø£»
=10£¬æɵƷ½³Ģ£¬øł¾Ż½ā·½³Ģ£¬æɵƓš°ø£»
£Ø3£©øł¾ŻPOÓėBQµÄŹ±¼äĻąµČ£¬æɵƷ½³Ģ£¬øł¾Ż½ā·½³Ģ£¬æɵƓš°ø£®
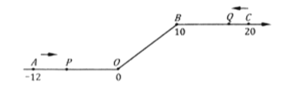
½ā£ŗ£Ø1£©µćPŌĖ¶ÆÖĮµćCŹ±£¬ĖłŠčŹ±¼ät£½12”Ā2£«10”Ā1£«10”Ā2£½21£ØĆė£©£¬
“š£ŗ¶ÆµćP“ÓµćAŌĖ¶ÆÖĮCµćŠčŅŖ21s £»
£Ø2£©ÓÉĢāŅāæɵĆ![]() £¬
£¬
![]() £¬
£¬![]() Į½µćŌŚĻ߶Ī
Į½µćŌŚĻ߶Ī![]() ÉĻĻąÓö
ÉĻĻąÓö
”ą![]() £¬
£¬
”ą![]() £¬
£¬
”ą![]() Ėł¶ŌµÄŹż×ÖĪŖ12-6=6;
Ėł¶ŌµÄŹż×ÖĪŖ12-6=6;
£Ø3£©µ±µć![]() ŌŚ
ŌŚ![]() ÉĻ£¬µć
ÉĻ£¬µć![]() ŌŚ
ŌŚ![]() ÉĻŹ±£¬
ÉĻŹ±£¬![]() £¬
£¬![]() £¬
£¬
”ß![]() £¬
£¬
”ą![]() £¬
£¬
”ą![]() £»
£»
µ±µć![]() ŌŚ
ŌŚ![]() ÉĻ£¬µć
ÉĻ£¬µć![]() ŌŚ
ŌŚ![]() ÉĻŹ±£¬
ÉĻŹ±£¬![]() £¬
£¬![]() £¬
£¬
”ß![]() £¬
£¬
”ą![]() £¬
£¬
”ą![]() £»
£»
µ±µć![]() ŌŚ
ŌŚ![]() ÉĻ£¬µć
ÉĻ£¬µć![]() ŌŚ
ŌŚ![]() ÉĻŹ±£¬
ÉĻŹ±£¬![]() £¬
£¬![]() £¬
£¬
”ß![]() £¬
£¬
”ą![]() £¬
£¬
”ą![]() £¬
£¬
µ±µć![]() ŌŚ
ŌŚ![]() ÉĻ£¬µć
ÉĻ£¬µć![]() ŌŚ
ŌŚ![]() ÉĻŹ±£¬
ÉĻŹ±£¬![]() £¬ĪŽ½ā
£¬ĪŽ½ā
µ±µć![]() ŌŚ
ŌŚ![]() ÉĻ£¬µć
ÉĻ£¬µć![]() ŌŚ
ŌŚ![]() ÉĻŹ±£¬
ÉĻŹ±£¬![]() £¬
£¬![]() £¬
£¬
”ß![]() £¬
£¬
”ą![]() £¬
£¬
”ą![]()
”ąµ±![]() Ź±£¬
Ź±£¬![]() £®
£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌĶĮĄķ½ā£ŗČōŅ»øöČżĪ»ŹżŹĒ312£¬Ōņ°ŁĪ»ÉĻŹż×ÖĪŖ3£¬Ź®Ī»ÉĻŹż×ÖĪŖ1£¬øöĪ»ÉĻŹż×ÖĪŖ2£¬ÕāøöČżĪ»ŹżæɱķŹ¾ĪŖ3”Į100+1”Į10+2£»ČōŅ»øöČżĪ»ŹżŹĒ©312£¬Ōņ°ŁĪ»ÉĻŹż×ÖĪŖ3£¬Ź®Ī»ÉĻŹż×ÖĪŖ1£¬øöĪ»ÉĻŹż×ÖĪŖ2£¬ÕāøöČżĪ»ŹżæɱķŹ¾ĪŖ©£Ø3”Į100+1”Į10+2£©£»
Ó¦ÓĆ£ŗÓŠŅ»øöÕżµÄĖÄĪ»Źż£¬Ē§Ī»ÉĻŹż×ÖĪŖa£¬°ŁĪ»ÉĻŹż×ÖĪŖb£¬Ź®Ī»ÉĻŹż×ÖĪŖc£¬øöĪ»Źż×ÖĪŖd£¬ĒŅa£¾d£¬b©c£¾1£®°“Ė³ŠņĶź³ÉŅ»ĻĀŌĖĖć£»
µŚŅ»²½£ŗ½»»»Ē§Ī»ŗĶøöĪ»ÉĻµÄŹż×ÖŅ²½»»»°ŁĪ»ŗĶŹ®Ī»ÉĻµÄŹż×Ö£¬¶ų¹¹³ÉĮķŅ»øöĖÄĪ»Źż£»
µŚ¶ž²½£ŗÓĆŌĖÄĪ»Źż¼õČ„µŚŅ»²½¹¹³ÉµÄĖÄĪ»Źż£¬°ŃÕāøöŠĀĖÄĪ»Źż¼ĒĪŖM£»
µŚČż²½£ŗ½»»»MµÄ°ŁĪ»ŗĶŹ®Ī»ÉĻµÄŹż×Ö£¬ÓÖ¹¹³ÉŅ»øöŠĀĖÄĪ»Źż£¬¼ĒĪŖN£»
µŚĖIJ棬½«MŗĶNĻą¼Ó
£Ø1£©µŚŅ»²½¹¹³ÉµÄĮķŅ»øöĖÄĪ»ŹżæɱķŹ¾ĪŖ”” ””£»
£Ø2£©ŹŌÅŠ¶ĻM°ŁĪ»ŗĶŹ®Ī»µÄŹż×ÖÖ®ŗĶŹĒ·ńĪŖ¶ØÖµ£æĒėĖµĆ÷ĄķÓÉ£®
£Ø3£©ČōMŗĶNĻą¼ÓµÄÖµĪŖ8892£¬Ēóa©dµÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ABŹĒ”ŃOµÄÖ±¾¶£¬CĪŖ”ŃOÉĻŅ»µć£¬CDĘ½·Ö”ĻACB½»”ŃOÓŚµćD£®
£Ø1£©ADÓėBDĻąµČĀš£æĪŖŹ²Ć“£æ
£Ø2£©ČōAB=10£¬AC=6£¬ĒóCDµÄ³¤£»
£Ø3£©ČōPĪŖ”ŃOÉĻŅģÓŚA”¢B”¢C”¢DµÄµć£¬ŹŌĢ½¾æPA”¢PD”¢PBÖ®¼äµÄŹżĮæ¹ŲĻµ£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
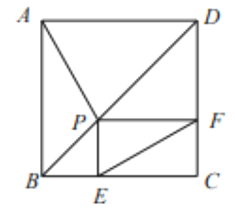
”¾ĢāÄæ”æČēĶ¼£¬¼ŗÖŖÕż·½ŠĪABCDµÄ±ß³¤ĪŖ4, PŹĒ¶Ō½ĒĻßBDÉĻŅ»µć£¬PE”ĶBCÓŚµćE, PF”ĶCDÓŚµćF,Į¬½ÓAP, EF.øų³öĻĀĮŠ½įĀŪ:¢ŁPD=![]() EC:¢ŚĖıߊĪPECFµÄÖܳ¤ĪŖ8;¢Ū”÷APDŅ»¶ØŹĒµČŃüČż½ĒŠĪ:¢ÜAP=EF£»¢ŻEFµÄ×īŠ”ÖµĪŖ
EC:¢ŚĖıߊĪPECFµÄÖܳ¤ĪŖ8;¢Ū”÷APDŅ»¶ØŹĒµČŃüČż½ĒŠĪ:¢ÜAP=EF£»¢ŻEFµÄ×īŠ”ÖµĪŖ![]() £»¢ŽAP”ĶEF.ĘäÖŠÕżČ·½įĀŪµÄŠņŗÅĪŖ£Ø £©
£»¢ŽAP”ĶEF.ĘäÖŠÕżČ·½įĀŪµÄŠņŗÅĪŖ£Ø £©
A. ¢Ł¢Ś¢Ü¢Ż¢ŽB. ¢Ł¢Ś¢Ü¢Ż
C. ¢Ś¢Ü¢ŻD. ¢Ś¢Ü¢Ż¢Ž
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬µćA£¬BŌŚŹżÖįÉĻ±ķŹ¾µÄŹż·Ö±šĪŖ-2Óė+6£¬¶ÆµćP“ÓµćA³ö·¢£¬ŃŲA”śBŅŌĆæĆė2øöµ„Ī»³¤¶ČµÄĖŁ¶ČĻņÖÕµćBŌĖ¶Æ£¬Ķ¬Ź±£¬¶ÆµćQ“ÓµćB³ö·¢£¬ŃŲB”śAŅŌĆæĆė4øöµ„Ī»³¤¶ČµÄĖŁ¶ČĻņÖÕµćAŌĖ¶Æ£¬µ±Ņ»øöµćµ½“ļŹ±£¬ĮķŅ»µćŅ²ĖęÖ®Ķ£Ö¹ŌĖ¶Æ.

£Ø1£©µ±QĪŖABµÄÖŠµćŹ±£¬ĒóĻ߶ĪPQµÄ³¤£»
£Ø2£©µ±QĪŖPBµÄÖŠµćŹ±£¬ĒóµćP±ķŹ¾µÄŹż.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ”°Čē¹ū¶ž“ĪŗÆŹży=ax2+bx+cµÄĶ¼ĻóÓėxÖįÓŠĮ½øö¹«¹²µć£¬ÄĒĆ“Ņ»ŌŖ¶ž“Ī·½³Ģax2+bx+c=0ÓŠĮ½øö²»ĻąµČµÄŹµŹżøł£®”±Ēėøł¾ŻÄć¶ŌÕā¾ä»°µÄĄķ½ā£¬½ā¾öĻĀĆęĪŹĢā£ŗČōm”¢n£Øm£¼n£©ŹĒ¹ŲÓŚxµÄ·½³Ģ1©£Øx©a£©£Øx©b£©=0µÄĮ½øł£¬ĒŅa£¼b£¬Ōņa”¢b”¢m”¢nµÄ“󊔹ŲĻµŹĒ£Ø £©£®
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
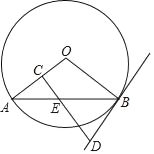
”¾ĢāÄæ”æČēĶ¼£¬ABŹĒ”ŃOµÄŅ»ĢõĻŅ£¬EŹĒABµÄÖŠµć£¬¹żµćE×÷EC”ĶOAÓŚµćC£¬¹żµćB×÷”ŃOµÄĒŠĻß½»CEµÄŃÓ³¤ĻßÓŚµćD£®
£Ø1£©ĒóÖ¤£ŗDB=DE£»
£Ø2£©ČōAB=12£¬BD=5£¬Ēó”ŃOµÄ°ė¾¶£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚÖ±ĻßLÉĻŅĄ“Ī°Ś·Å×ÅĘßøöÕż·½ŠĪ£¬ŅŃÖŖŠ±·ÅÖƵÄČżøöÕż·½ŠĪµÄĆ껿·Ö±šĪŖ1”¢2”¢3£¬Õż·ÅÖƵÄĖÄøöÕż·½ŠĪµÄĆ껿ŅĄ“ĪŹĒS1”¢S2”¢S3”¢S4 £¬ ŌņS1+2S2+2S3+S4=£Ø£©
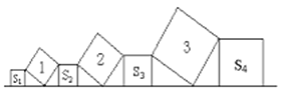
A. 5 B. 4 C. 6 D. 10
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚÕż·½ŠĪABCDÖŠ£¬OŹĒ¶Ō½ĒĻßACÓėBDµÄ½»µć£¬MŹĒBC±ßÉĻµÄ¶Æµć£ØµćM²»ÓėB”¢CÖŲŗĻ£©£¬CN”ĶDM£¬CNÓėAB½»ÓŚµćN£¬Į¬½ÓOM”¢ON”¢MN.ĻĀĮŠĖÄøö½įĀŪ£ŗ¢Ł”÷CNB”Õ”÷DMC£»¢Ś”÷CON”Õ”÷DOM£»¢ŪAN2£«CM2£½MN2£»¢ÜČōAB£½2£¬ŌņS”÷OMNµÄ×īŠ”ÖµŹĒ![]() .ĘäÖŠÕżČ·½įĀŪµÄøöŹżŹĒ£Ø £©
.ĘäÖŠÕżČ·½įĀŪµÄøöŹżŹĒ£Ø £©
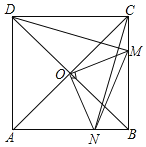
A.1B.2C.3D.4
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com