
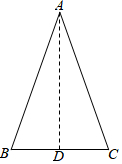
 命题:有两个角相等的三角形是等腰三角形(简称“等角对等边”).
命题:有两个角相等的三角形是等腰三角形(简称“等角对等边”).分析 (1)根据AAS即可判断;
(2)过点D作DE⊥AB于点E,过点D作DF⊥AC于点F.首先证明△BDE≌△CDF(AAS),推出BE=CF,DE=DF,再证明Rt△AED≌Rt△AFD,推出AE=AF即可解决问题;
解答 解:(1)△ABD≌△ACD的理由是AAS,
故答案为AAS.
(2)证明:过点D作DE⊥AB于点E,过点D作DF⊥AC于点F.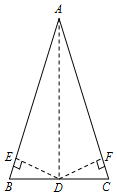
∵∠BED=∠CFD=90°,∠B=∠C,BD=CD.
∴△BDE≌△CDF(AAS).
∴BE=CF,DE=DF.
在Rt△AED和Rt△AFD中,∠AED=∠AFD=90°.
∵AD=AD,DE=DF,
∴Rt△AED≌Rt△AFD.
∴AE=AF.
∴AE+BE=AF+CF.
即AB=AC.
点评 本题考查全等三角形的判定和性质,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
| 方案一 | A | B | |
| 标价(单位:元) | 90 | 100 | |
| 每件商品返利 | 按标价的30% | 按标价的15% | |
| 例:买一件A商品,只需付款90(1-30%)元 | |||
| 方案二 | 若所购商品达到或超过100件(不同商品可累计),则按标价的20%返利. | ||
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
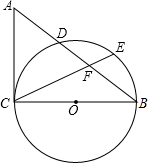 如图,△ABC中,以BC为直径的半圆O交AB于点D.点E为$\widehat{BD}$的中点,CE与AB交于点F,且AF=AC.
如图,△ABC中,以BC为直径的半圆O交AB于点D.点E为$\widehat{BD}$的中点,CE与AB交于点F,且AF=AC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com