解:(1)由于抛物线的图象经过B(-2,0),C(4,0)两点,则有:
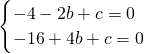
,
解得
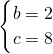
;
故抛物线的解析式为:y=-x
2+2x+8.
(2)易知抛物线的对称轴为:x=1;
设点T(1,m),
则直线BT的斜率:k
1=
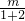
,直线CT的斜率:k
2=

;
若⊙B与CT相切,则有:
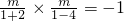
,
解得m=±3;
故T(1,3)或(1,-3).
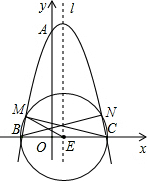
(3)以E为圆心,BC长为直径作圆,交抛物线于M、N两点;
由圆周角定理知:∠BMC=∠BNC=90°,
此时ME=NE=

BC=3;
若∠BPC是锐角,那么点P必在M、N之间的抛物线图象上,故PE>3;
易知抛物线的顶点坐标为:(1,9),
当点P运动到抛物线的顶点位置时,PE的长最大,且此时PE=9;
综上可知,PE的取值范围为:3<PE≤9.
(4)法一:由y=-x
2+2x+8,故关于x的一元二次方程x
2-2x+(y-8)=0有整数解,
因此△
x=4-4(y-8)=-4y+36是完全平方数,且△
x=-4y+36≥0,
则y≤9,又y是一个完全平方数,
所以,y只能为0,1,4,9;
分别代入方程x
2-2x+(y-8)=0,又x为整数,
解得
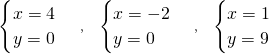
,
因此m=4、n=-2、s=1.
法二:由图象不难看出0≤y≤9,又y是一个完全平方数,
所以y只能为0,1,4,9,
分别代入关系式y=-x
2+2x+8,又x为整数,
解得
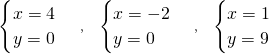
,
因此m=4、n=-2、s=1.
分析:(1)将B、C坐标代入抛物线的解析式中,通过联立方程组即可确定该抛物线的解析式.
(2)若⊙B与直线CT相切,那么BT⊥CT,易得抛物线的对称轴方程,可设出点T的纵坐标,利用直线BT、直线CT的垂直,即斜率的乘积为-1,即可列出关于T点纵坐标的方法,求得点T的坐标.
(3)此题应该结合圆周角定理来理解,以E为圆心,BC为半径作圆,交抛物线于M、N两点,那么∠BMC=∠BNC=90°,若∠BEC是锐角,那么点E必在M、N之间的函数图象上,当P位于M或N得位置时,PE=3,当P位于抛物线的顶点时,PE的值为抛物线顶点纵坐标,由此可求得PE的取值范围.
(4)将(1)题所得抛物线解析式化为关于x的一元二次方程,由于方程有整数解,那么根的判别式大于0,可据此求得y的取值范围,由于y是一个完全平方数,进而可求得y的值,再将其值代入方程中即可求得x的值,从而确定m、n、s的值.(也可通过观察函数图象来确定y的值)
点评:此题考查了二次函数解析式的确定、切线的性质、圆周角定理、直角三角形的性质、根的判别式等重要知识;涉及的知识点较多,综合性强,难度较大.

 交点.
交点.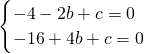 ,
,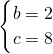 ;
;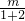 ,直线CT的斜率:k2=
,直线CT的斜率:k2= ;
;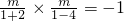 ,
,
 BC=3;
BC=3;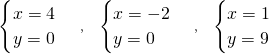 ,
,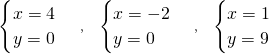 ,
,

 (2013•莒南县二模)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:
(2013•莒南县二模)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论: 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①ac>0;②a-b+c<0;
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①ac>0;②a-b+c<0;