
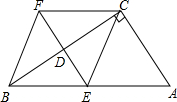
 如图所示,在四边形ABFC,∠ACB=90°,BC垂直平分线EF交BC于点D,交AB于点E,且CF=AE
如图所示,在四边形ABFC,∠ACB=90°,BC垂直平分线EF交BC于点D,交AB于点E,且CF=AE分析 (1)根据中垂线的性质:中垂线上的点到线段两个端点的距离相等,有BE=EC,BF=FC,又因为CF=AE,BE=EC=BF=FC,根据四边相等的四边形是菱形,所以四边形BECF是菱形;
(2)由菱形的性质知,对角线平分一组对角,即当∠ABC=45°时,∠EBF=90°,有菱形为正方形,根据直角三角形中两个角锐角互余得,∠A=45度.
解答 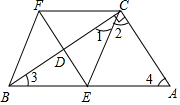 解:(1)四边形BECF是菱形.
解:(1)四边形BECF是菱形.
∵EF垂直平分BC,
∴BF=FC,BE=EC,
∴∠3=∠1,
∵∠ACB=90°,
∴∠3+∠4=90°,∠1+∠2=90°,
∴∠2=∠4,
∴EC=AE,
∴BE=AE,
∵CF=AE,
∴BE=EC=CF=BF,
∴四边形BECF是菱形.
(2)当∠A=45°时,菱形BECF是正方形.
证明:∵∠A=45°,∠ACB=90°,
∴∠1=45°,
∴∠EBF=2∠A=90°,
∴菱形BECF是正方形.
点评 本题考查菱形的判定和性质以及正方形的判定,有一定难度,解题关键是熟练掌握菱形的判定方法及性质并灵活运用.


 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:解答题
| 摸球总次数 | 20 | 30 | 60 | 90 | 120 | 180 | 240 | 330 | 450 |
| “和为6”出现的频数 | 10 | 13 | 24 | 30 | 37 | 58 | 82 | 110 | 150 |
| “和为6”出现的频数 | 0.50 | 0.43 | 0.40 | 0.33 | 0.31 | 0.32 | 0.34 | 0.33 | 0.33 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
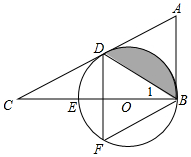 如图,在△ABC中,∠ABC=90°,D是AC边上一点,连接BD,使∠A=2∠1,E是BC上的一点,以BE为直径的⊙O经过点D,点F在弧DEB上.
如图,在△ABC中,∠ABC=90°,D是AC边上一点,连接BD,使∠A=2∠1,E是BC上的一点,以BE为直径的⊙O经过点D,点F在弧DEB上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2a3-3a2 | B. | 2a3-3a2+1 | C. | 3a3-6a2+1 | D. | 以上都不对 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a>b | B. | a<b | ||
| C. | a=b | D. | 与a、b的大小关系无关 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com