
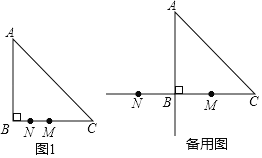
【题目】在△ABC中,∠ABC=90°,AB=BC=2,点M是线段BC的中点,点N在射线MB上,连接AN,平移△ABN,使点N移动到点M,得到△DEM(点D与点A对应,点E与点B对应),DM交AC于点P.
(1)若点N是线段MB的中点,如图1.
①依题意补全图1;
②求DP的长;
(2)若点N在线段MB的延长线上,射线DM与射线AB交于点Q,若MQ=DP,求CE的长.
【答案】(1)①见解析,②![]() ;(2)2
;(2)2![]() ﹣2
﹣2
【解析】
(1)利用平移的性质画出图形,再利用相似得出比例式,即可求出线段DP的长;
(2)根据条件MQ=DP,利用平行四边形的性质和相似三角形的性质,求出BN的长即可解决.
解:(1)①如图1,补全图形:
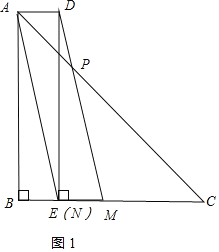
②连接AD,如图1,
在Rt△ABN中,
∵∠B=90°,AB=4,BN=1,
∴AN=![]() ,
,
∵线段AN平移得到线段DM,
∴DM=AN=![]() ,
,
由平移可得,AD=NM=1,AD∥MC,
∴△ADP∽△CMP,
∴![]() ,
,
∴DP=![]() DM=
DM=![]() ;
;
(2)如图2,连接NQ,
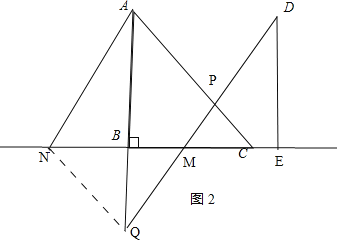
由平移知:AN∥DM,且AN=DM,
∵MQ=DP,
∴PQ=DM,
∴AN∥PQ,且AN=PQ,
∴四边形ANQP是平行四边形,
∴NQ∥AP,
∴∠BQN=∠BAC=45°,
又∵∠NBQ=∠ABC=90°,
∴BN=BQ,
∵AN∥MQ,
∴![]() ,
,
又∵M是BC的中点,且AB=BC=4,
∴![]() ,
,
∴NB=2 ![]() 或-2
或-2 ![]() (舍去),
(舍去),
∴ME=BN=2![]() ,
,
∴CE=2![]() ﹣2.
﹣2.


科目:初中数学 来源: 题型:
【题目】某竹制品加工厂根据市场调研结果,对该厂生产的一种新型竹制品玩具未来两年的销售进行预测,并建立如下模型:设第t个月,竹制品销售量为P(单位:箱),P与t之间存在如图所示函数关系,其图象是线段AB(不含点A)和线段BC的组合.设第t个月销售每箱的毛利润为Q(百元),且Q与t满足如下关系Q=2t+8(0≤t≤24).
(1)求P与t的函数关系式(6≤t≤24).
(2)该厂在第几个月能够获得最大毛利润?最大毛利润是多少?
(3)经调查发现,当月毛利润不低于40000且不高于43200元时,该月产品原材料供给和市场售最和谐,此时称这个月为“和谐月”,那么,在未来两年中第几个月为和谐月?

查看答案和解析>>
科目:初中数学 来源: 题型:
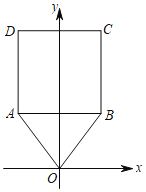
【题目】如图,平面直角坐标系中,已知O(0,0),A(﹣3,4),B(3,4),将△OAB与正方形ABCD组成的图形绕点O顺时针旋转,每次旋转90°,测第70次旋转结束时,点D的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
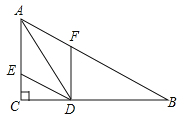
【题目】如图,在△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,DE∥BA交AC于点E,DF∥CA交AB于点F,已知CD=3.
(1)求AD的长;
(2)求四边形AEDF的周长.(注意:本题中的计算过程和结果均保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:关于x的方程mx2-3(m+1)x+2m+3=0(m≠0).
(1)若方程有两个相等的实数根,求m的值;
(2)求此方程的两个根(若所求方程的根不是常数,就用含m的式子表示);
(3)若m为整数,当m取何值时方程的两个根均为正整数?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年元且,某商场为促销举办抽奖活动.规则如下:在一个不透明的纸盒里,装有2个红球和2个黑球,这些球除颜色外都相同.顾客每次摸出1个球,若摸到红球,则获得一份奖品;若摸到黑球,则没有奖品.
(1)如果张大妈只有一次摸球机会,那么张大妈获得奖品的概率是 .
(2)如果张大妈有两次摸球机会(摸出后不放回),请用“树状图”或“列表”的方法,求张大妈获得两份奖品的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
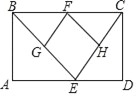
【题目】已知矩形ABCD中,E是AD边上的一个动点,点F,G,H分别是BC,BE,CE的中点.
(1)求证:△BGF≌△FHC;
(2)设AD=a,当四边形EGFH是正方形时,求矩形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,抛物线![]() 与
与![]() 轴交于点A和点C(2,0),与
轴交于点A和点C(2,0),与![]() 轴交于点D,将△DOC绕点O逆时针旋转90°后,点D恰好与点A重合,点C与点B重合.
轴交于点D,将△DOC绕点O逆时针旋转90°后,点D恰好与点A重合,点C与点B重合.
(1)直接写出点A和点B的坐标;
(2)求![]() 和
和![]() 的值;
的值;
(3)已知点E是该抛物线的顶点,求证:AB⊥EB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义两个不相交的函数图象在竖直方向上的最短距离为这两个函数的“和谐值”.
(1)求抛物线y=x2﹣2x+2与x轴的“和谐值”;
(2)求抛物线y=x2﹣2x+2与直线y=x﹣1的“和谐值”.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com