
【题目】如图,△ABC中,AD是高,CE是中线,点G是CE的中点,DG⊥CE,点G为垂足.

(1)求证:DC=BE;
(2)若∠AEC=69°,求∠EDG的度数.
【答案】(1)详见解析;(2)67°
【解析】
(1)由G是CE的中点,DG⊥CE得到DG是CE的垂直平分线,根据线段垂直平分线的性质得到DE=DC,由DE是Rt△ADB的斜边AB上的中线,根据直角三角形斜边上的中线等于斜边的一半得到DE=BE=![]() AB,即可得到DC=BE;
AB,即可得到DC=BE;
(2)由DE=DC得到∠DEC=∠BCE,由DE=BE得到∠B=∠EDB,根据三角形外角性质得到∠EDB=∠DEC+∠BCE=2∠BCE,则∠B=2∠BCE,由此根据外角的性质来求∠BCE的度数即可解决问题.
解:(1)如图,∵G是CE的中点,DG⊥CE,
∴DG是CE的垂直平分线,
∴DE=DC,
∵AD是高,CE是中线,
∴DE是Rt△ADB的斜边AB上的中线,
∴DE=BE=![]() AB,
AB,
∴DC=BE;
(2)∵DE=DC,
∴∠DEC=∠BCE,
∴∠EDB=∠DEC+∠BCE=2∠BCE,
∵DE=BE,
∴∠B=∠EDB,
∴∠B=2∠BCE,
∴∠AEC=3∠BCE=69°,
∴∠BCE=23°,
∵∠DGC=90°,
∴∠GDC=67°,
∵DE=DC,EG=CG,
∴∠EDG=∠GDC=67°.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某地电话拨号入网有两种收费方式,用户可以任选其一.
计时制:0.05元/分;
包月制:50元/月(限一部个人住宅电话上网).
此外,每一种上网方式都得加收通信费0.02元/分.
(1)某用户某月上网的时间为x小时,请你分别写出两种收费方式下该用户应该支付的费用.
(2)若某用户估计一个月内上网的时间为20小时,你认为采用哪种方式较为合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课堂上,数学老师提出了如下问题:
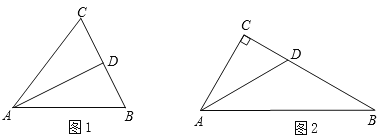
如图1,若线段AD为△ABC的角平分线,请问![]() 一定成立吗?
一定成立吗?
小明和小芳分别作了如下探究:
小明发现:如图2,当△ABC为直角三角形时,且∠C=90°,∠CAB=60°时,结论成立;
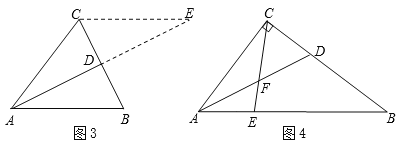
小芳发现:如图3,当△ABC为任意三角形时,过点C作AB的平行线,交AD的延长线于点E,利用此图可以证明![]() 成立.
成立.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车从![]() 地出发,匀速驶向
地出发,匀速驶向![]() 地.甲车以
地.甲车以![]() 的速度行驶
的速度行驶![]() 后,乙车沿相同的路线出发.乙车先到达
后,乙车沿相同的路线出发.乙车先到达![]() 地并停留
地并停留![]() 后,再以原来的速度按原路线返回,直到与甲车相遇.在这个过程中,两车之间的距离
后,再以原来的速度按原路线返回,直到与甲车相遇.在这个过程中,两车之间的距离![]() 与乙车行驶的时间
与乙车行驶的时间![]() 之间的函数关系如图所示,则当两车相距
之间的函数关系如图所示,则当两车相距![]() 时,乙车出发的时间为______
时,乙车出发的时间为______![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形EFGH是矩形ABCD的内接矩形,且EF:FG=3:1,AB:BC=2:1,则tan∠AHE的值为( ).

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,O是坐标原点,一次函数y=kx+b的图象与x轴交于点A(﹣3,0),与y轴交于点B,且与正比例函数y=![]() x的图象的交点为C(m,4).
x的图象的交点为C(m,4).

(1)求一次函数y=kx+b的解析式;
(2)D是平面内一点,以O、C、D、B四点为顶点的四边形是平行四边形,直接写出点D的坐标.(不必写出推理过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①是一个直角三角形纸片,∠C=90°,AB=13cm,BC=5cm,将其折叠,使点C落在斜边上的点C′处,折痕为BD(如图②),求DC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,连结AD1、BC1.已知∠ACB=30°,AB=1,
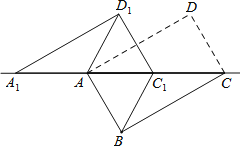
(1)求证:△A1AD1≌△CC1B;
(2)当CC1=1时,求证:四边形ABC1D1是菱形。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com