
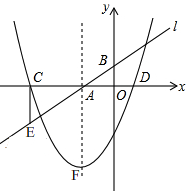
 如图1,直线l:y=mx+n交x轴,y轴于点A,B,抛物线与x轴交于点C、D,对称轴经过点A,顶点F的纵坐标为-3.CE⊥x轴交直线l于点E(-5,-$\frac{3}{2}$),tan∠BAD=$\frac{1}{2}$.
如图1,直线l:y=mx+n交x轴,y轴于点A,B,抛物线与x轴交于点C、D,对称轴经过点A,顶点F的纵坐标为-3.CE⊥x轴交直线l于点E(-5,-$\frac{3}{2}$),tan∠BAD=$\frac{1}{2}$.分析 (1)先确定出点A,B坐标,利用三角函数得出m,再利用点E在直线l上,进而确定出m,即可得出直线l的解析式,再用待定系数法确定出抛物线解析式;
(2)先设出点P的坐标,用面积建立方程即可确定出P的坐标;
(3)设出M,先根据点M,N的位置得出AM是平行四边形的对角线,即可得出AM的中点也是BN的中点,确定出点N的坐标,用二次函数关系式建立方程即可确定出点M的坐标.
解答 解:(1)如图1,∵直线l:y=mx+n交x轴,y轴于点A,B,
∴B(0,n),A(-$\frac{n}{m}$,0),
∴OB=n,OA=$\frac{n}{m}$,
∵tan∠BAD=$\frac{OB}{OA}$=$\frac{1}{2}$,
∴$\frac{n}{m}$=2n,
∴m=$\frac{1}{2}$,
∵点E(-5,-$\frac{3}{2}$),
∴-5m+n=-$\frac{3}{2}$,
∴n=1,
∴直线l的解析式为y=$\frac{1}{2}$x+1;
∴A(-2,0),
∴F(-2,-3),
∵CE⊥x轴,
∴C(-5,0),
∴D(1,0),
设抛物线的表达式为y=a(x+2)2-3,
∵点D在抛物线上,
∴a(1+2)2-3=0,
∴a=$\frac{1}{3}$,
∴抛物线的表达式为y=$\frac{1}{3}$(x+2)2-3,
(2)∵E(-5,-$\frac{3}{2}$),
∴CE=$\frac{3}{2}$,设点P(p,$\frac{1}{3}$(p+2)2-3),
∵S△CEP=3,
∴$\frac{1}{2}$CE×|p+5|=$\frac{1}{2}$×$\frac{3}{2}$×|p+5|=3,
∴p=-1或p=-9,
∴P(-1,-$\frac{8}{3}$)或(-9,$\frac{40}{3}$);
(3)∵以点A、B、M、N为顶点的四边形是平行四边形,且点M在x轴上,点N在x轴下方的抛物线上,
∴AM必是平行四边形的对角线的交点,
∴BN过线段AM的中点G,设点M(a,0),
∴G($\frac{a-2}{2}$,0),N(a-2,-1),
∵点N在抛物线y=$\frac{1}{3}$(x+2)2-3上,
∴$\frac{1}{3}$(a-2+2)2-3=-1,
∴a=±$\sqrt{6}$,
∴M(-$\sqrt{6}$,0)或($\sqrt{6}$,0).
点评 此题是二次函数综合题,主要考查了待定系数法,三角函数,三角形的面积公式,平行四边形的性质,解本题的关键是确定出抛物线解析式,是一道中等难度的中考常考题.


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案科目:初中数学 来源: 题型:解答题
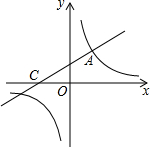 直线y=$\frac{1}{2}$x+2与双曲线y=$\frac{k}{x}$相交于点A(2,3).
直线y=$\frac{1}{2}$x+2与双曲线y=$\frac{k}{x}$相交于点A(2,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
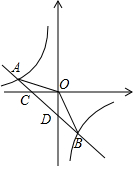 如图,在平面直角坐标系中,一次函数y=ax-1(a≠0)的图象与x轴交于点C,与y轴交于点D,与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于第二、四象限内的A、B两点,点B的坐标是(3,m),连接OB,tan∠BOD=$\frac{3}{4}$.
如图,在平面直角坐标系中,一次函数y=ax-1(a≠0)的图象与x轴交于点C,与y轴交于点D,与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于第二、四象限内的A、B两点,点B的坐标是(3,m),连接OB,tan∠BOD=$\frac{3}{4}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com