【题目】如图，在正方形
内有一点
满足
，
.连接
、
.
（1）求证：
；
（2）求
的度数.
【答案】（1）见解析；（2）15°
【解析】
（1）根据PB=PC得∠PBC=∠PCB，从而可得∠ABP=∠DCP，再利用SAS证明即可；
（2）由（1）得△PAD为等边三角形，可求得∠PAB=30°，∠PAC=∠PAD-∠CAD，因此可得结果．
解：（1）∵四边形ABCD为正方形，
∴∠ABC=∠DCB=90°，AB=CD，
∵BP=PC，
∴∠PBC=∠PCB，
∴∠ABP=∠DCP，
又∵AB=CD，BP=CP，
在△APB和△DPC中，
，
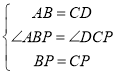∴△APB≌△DPC（SAS）；
（2）由（1）得AP=DP=AB=AD，
∴△PAD为等边三角形，
∴∠PAD=60°，∠PAB=30°，
在正方形ABCD中，∠BAC=∠DAC=45°，
∴∠PAC=∠PAD-∠CAD=60°-45°=15°.
阳光课堂同步练习系列答案科目：初中数学 来源： 题型：
【题目】把下列各数填在相应的大括号中：8，﹣
，+2.8，π，
，﹣0.003，0，﹣100，﹣3.626626662……
正数集合{_____ …}
整数集合{_____…}
负分数集合{_____ …}
无理数集合{_____ …}．
查看答案和解析>>
科目：初中数学 来源： 题型：
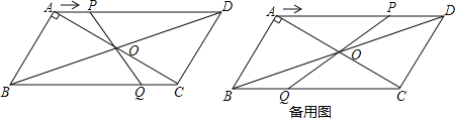
【题目】 如图，在ABCD中，对角线AC，BD相交于点O，AB⊥AC，AB=3cm，BC=5cm．点P从A点出发沿AD方向匀速运动速度为lcm/s，连接PO并延长交BC于点Q．设运动时间为t（s）（0＜t＜5）
（1）当t为何值时，四边形ABQP是平行四边形？
（2）设四边形OQCD的面积为y（cm2），当t=4时，求y的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知点（﹣1，y1），（2，y2），
在反比例函数y＝﹣
的图象上，则下列关系式正确的是（ ）
A.y3＜y2＜y1B.y2＜y3＜y1
C.y3＜y1＜y2D.y2＜y1＜y3
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在研究气体压强和体积关系的物理实验中，一个气球内充满了一定质量的气体，实验中气体温度保持不变，实验人员记录了实验过程中气球内的气体压强p（kPa）与气体体积V（m3）的数据如下表：
V（m3） | 0.8 | 1.2 | 1.6 | 2.0 | 2.4 |
p（kPa） | 120 | 80 | 60 | 48 | 40 |
（1）根据表中的数据判断p是V的________．（①一次函数；②反比例函数；③二次函数．填序号即可）
（2）确定p与V的函数关系式，并在如图所示的坐标系内画出该函数的大致图象；
（3）当气球内的气体压强大于140kPa时，气球将爆炸，为了安全起见，气体的体积V（m3）的取值范围是________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某商店购进一批进价为20元/件的日用商品，第一个月，按进价提高50%的价格出售，售出400件；第二个月，商店准备在不低于原售价的基础上进行加价销售，根据销售经验，提高销售单价会导致销售量的减少．销售量y(件)与销售单价x(元)的关系如图所示．
(1)求y与x之间的函数表达式；
(2)第二个月的销售单价定为多少元时，可获得最大利润？最大利润是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，P为⊙O的直径BA延长线上的一点，PC与⊙O相切，切点为C，点D是⊙上一点，连接PD．已知PC=PD=BC．下列结论：
（1）PD与⊙O相切；（2）四边形PCBD是菱形；（3）PO=AB；（4）∠PDB=120°．
其中正确的个数为（ ）
A．4个 B．3个 C．2个 D．1个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】一块长方体木块的各棱长如图所示，一只蜘蛛在木块的一个顶点A处，一只苍蝇在这个长方体上和蜘蛛相对的顶点B处，蜘蛛急于捉住苍蝇，沿着长方体的表面向上爬．
(1)如果D是棱的中点，蜘蛛沿“AD→DB”路线爬行，它从A点爬到B点所走的路程为多少？
(2)若蜘蛛还走前面和右面这两个面，你认为“AD-DB"是最短路线吗？如果不是，请求出最短路程，如果是，请说明理由
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如下图，搭一个正方形需要4根火柴棒，搭2个正方形需要7根火柴棒，搭3个正方形需要10根火柴棒．
……
(1)若搭5个这样的正方形，这需要 根火柴棒；
(2)若搭n个这样的正方形，这需要 根火柴棒；
(3)若现在有2018根火柴棒，要搭700个这样的正方形，至少还需要火柴多少根？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com