练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知表示有理数a、b的点在数轴上的位置如图所示：

    则下列结论正确的是

    A. |a|<1<|b| B. 1<a<b C. 1<|a|<b D. -b<-a<-1

    C 【解析】试题解析：∵由图可知，a＜-1＜1＜b，1<|a|＜b， ∴-b＜a＜-1，1＜-a＜b，故A、B、D错误，C正确. 故选C．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：江苏省2018届九年级上学期期末模拟数学试卷（解析版） 题型：填空题

    将二次函数化成的形式应为__________．

    【解析】将二次函数配方可得, 故答案为: .

    查看答案和解析>>

    科目：初中数学 来源：四川省2017-2018学年八年级上学期期末考试数学试卷 题型：解答题

    解下列方程（不等式）组.

    (1)解方程组：

    (2) 解不等式组： ，并求其非负整数解.

    （1）（2）0，1, 2 【解析】试题分析：（1）方程①×3，然后利用加减消元法进行求解即可； （2）分别求出每一个不等式的解集，然后确定不等式组的解集，最后确定非负整数解即可. 试题解析：（1）， 由①×3+②，得： ， ， 把代入①得： ， ， 所以，原方程组的解为； （2）， 解不等式①，得： ， 解不等式②，得： ， 所以，不等式...

    查看答案和解析>>

    科目：初中数学 来源：山东省滨州市惠民县2017-2018学年七年级上学期期末数学试卷 题型：解答题

    列方程解应用题：

    A车和B车分别从甲，乙两地同时出发，沿同一路线相向匀速而行.出发后1.5小时两车相距75公里，之后再行驶2.5小时A车到达乙地，而B车还差40公里才能到达甲地.求甲地和乙地相距多少公里？

    甲地和乙地相距240公里. 【解析】试题分析：设甲地和乙地相距x千米，根据甲、乙两地的距离不变列出方程并解答．需要分类讨论：相遇前和相遇后相距75千米． 试题解析：设甲乙两地相距x千米， ①当相遇前相距75千米时， 依题意得： ， 解得x=240． ②当相遇后相距75千米时， 依题意得： ， 解得x=-400（舍去）． 答：甲地和乙地相距240...

    查看答案和解析>>

    科目：初中数学 来源：山东省滨州市惠民县2017-2018学年七年级上学期期末数学试卷 题型：填空题

    某同学在计算10+2x的值时，误将“+”看成了“﹣”，计算结果为20，那么10+2x的值应为___________．

    0 【解析】试题解析：根据题意得：10-2x=20， 解得x=-5， 则10+2x=10-10=0. 故答案为：0.

    查看答案和解析>>

    科目：初中数学 来源：山东省滨州市惠民县2017-2018学年七年级上学期期末数学试卷 题型：单选题

    下列方程：（1）2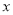－1＝－7，（2）＝－1，（3）2（＋5）＝－4－，（4）＝－2.其中解为＝－6的方程的个数为

    A. 4 B. 3 C. 2 D. 1

    C 【解析】试题解析：（1）2－1= －7， 移项得：2x-x=-7+1 化简得：x=-6； （2）－1， 移项得： =－1， 化简得： ∴x=-6； （3）2（＋5）=－4－， 去括号得：2x+10=-4-x 移项得：2x+x=-10-4 合并同类项得：3x=-14 系数化为1，得： （4）－2. 移项得： ...

    查看答案和解析>>

    科目：初中数学 来源：湖南省2018届九年级上学期期末考试数学试卷 题型：解答题

    如图，BC是⊙O的直径，A是弦BD延长线上一点，切线DE平分AC于E。

    （1）求证：AC是⊙O的切线；

    （2）若AD:DB=3:2，AC=15，求⊙O的直径。

    （1）连接OD、CD，先根据切线的性质得到OD⊥DE，即∠1+∠2=90°，再根据圆周角定理可得∠BDC=90°，再结合E为AC的中点，根据直角三角形的性质可得DE=CE=AE=AC，即得∠2=∠3，根据元的基本性质可得∠1=∠4，即得∠3+∠4=∠1+∠2=90°，从而证得结论；（2） 【解析】 试题分析：（1）连接OD、CD，先根据切线的性质得到OD⊥DE，即∠1+∠2=90°，再...

    查看答案和解析>>

    科目：初中数学 来源：湖南省2018届九年级上学期期末考试数学试卷 题型：单选题

    在Rt△ABC中，∠C=900，∠B=2∠A，则cosB等于（ ）

    A. B. C. D.

    B 【解析】∵∠C=90°， ∴∠A+∠B=90°， ∵∠B=2∠A， ∴∠A+2∠A=90°， ∴∠A=30°， ∴∠B=60°， ∴cosB=. 故选B.

    查看答案和解析>>

    科目：初中数学 来源：江苏省兴化市顾庄学区2017-2018学年八年级上学期期末考试数学试卷 题型：解答题

    如图，把矩形纸片ABCD沿EF折叠后，使得点D与点B重合，点C落在点C′的位置上．

    （1）△BEF是等腰三角形吗？试说明理由；

    （2）若AB＝4，AD＝8，求CF的长度．

    见解析 【解析】试题分析：（1）由AD∥BC得到∠1=∠2，由折叠性质得到∠2=∠FEB，则∠1=∠FEB，于是可判断△EBF是等腰三角形； （2）设BE=x，则DE=x，AE=AD﹣DE=8﹣x，在Rt△ABE中，理由勾股定理得到（8﹣x）2+42=x2，解得x=5，而△EBF是等腰三角形，所以BF=BE=5，即可得到CF的长． 试题解析：【解析】 （1）△BEF是等腰三角形...

    查看答案和解析>>

    同步练习册答案