
【题目】如图,OB是∠AOC的平分线,OD是∠COE的平分线.
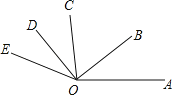
(1)若∠AOB=40°,∠DOE=30°,求∠BOD的度数;
(2)若∠AOD与∠BOD互补,且∠DOE=35°,求∠AOC的度数.
【答案】(1)∠BOD=70°;(2)∠AOC=![]() .
.
【解析】
(1)由图可知∠BOD=∠COD+∠COB,根据角平分线的定义∠COD,∠COB的度数都可求,所以∠BOD的度数也可求.
(2)可设∠AOB=x,然后利用角平分线的定义及∠DOE表示出∠AOD与∠BOD,然后利用∠AOD与∠BOD互补建立方程,解方程即可求出x的值,从而∠AOC的度数可求.
(1)∵OB是∠AOC的平分线,OD是∠COE的平分线
∴∠COB=∠BOA=40°,∠COD=∠DOE=30°
∴∠BOD=∠COD+∠COB=70°;
(2)由题意得:∠AOD+∠BOD=180°,
∵OD平分∠COE,∠DOE=35°,
∴∠COD=∠DOE=35°,
设∠AOB=x,则∠AOD=2x+35°,∠BOD=x+35°,
∴2x+35°+x+35°=180°,
解得:x=![]() ,
,
∴∠AOC=2x=![]() .
.


 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在数轴上,点A、B对应的数分别为a、b,且a、b满足|a+4|+(b﹣8)2=0.
(1)求A、B所表示的数;
(2)若点C在数轴上对应的数为x,且x是方程2x+1=![]() x﹣8的解.
x﹣8的解.
①求线段BC的长;
②在数轴上是否存在点P,使PA+PB=BC?若存在,求出点P对应的数;若不存在,说明理由.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
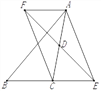
【题目】如图,在△ABC中,D是AC的中点,E是线段BC延长线上一点,过点A作BE的平行线与线段ED的延长线交于点F,连接AE、CF.
(1)求证:AF=CE;
(2)如果AC=EF,且∠ACB=135°,试判断四边形AFCE是什么样的四边形,并证明你的结论
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段CD在线段AB上,且CD=2,若线段AB的长度是一个正整数,则图中以A,B,C,D这四点中任意两点为端点的所有线段长度之和可能是( )![]()
A. 29
B. 28
C. 30
D. 31
查看答案和解析>>
科目:初中数学 来源: 题型:
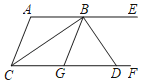
【题目】如图,AE∥CF,∠ACF的平分线交AE于点B,G是CF上的一点,∠GBE的平分线交CF于点D,且BD⊥BC,下列结论:①BC平分∠ABG;②AC∥BG;③与∠DBE互余的角有2个;④若∠A=α,则∠BDF=![]() .其中正确的有_____.(把你认为正确结论的序号都填上)
.其中正确的有_____.(把你认为正确结论的序号都填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
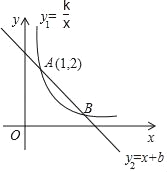
【题目】反比例函数y1=![]() (x>0)的图象与一次函数y2=﹣x+b的图象交于A,B两点,其中A(1,2)
(x>0)的图象与一次函数y2=﹣x+b的图象交于A,B两点,其中A(1,2)
(1)求这两个函数解析式;
(2)在y轴上求作一点P,使PA+PB的值最小,并直接写出此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条不完整的数轴上从左到右有点A,B,D,C,其中AB=2,BD=3,DC=1,如图所示,设点A,B,D,C所对应数的和是p.
![]()
(1)若以B为原点.写出点A,D,C所对应的数,并计算p的值;
(2)①若原点O在图中数轴上点C的右边,且CO=x,p=﹣71,求x.
②此时,若数轴上存在一点E,使得AE=2CE,求点E所对应的数(直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
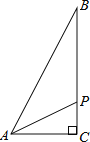
【题目】在![]() 中,
中,![]() ,点P从点A出发,以
,点P从点A出发,以![]() 的速度沿折线
的速度沿折线![]() 运动,最终回到点A,设点P的运动时间为
运动,最终回到点A,设点P的运动时间为![]() ,线段AP的长度为
,线段AP的长度为![]() ,则能够反映y与x之间函数关系的图象大致是
,则能够反映y与x之间函数关系的图象大致是![]()
A. 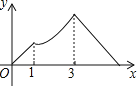 B.
B. 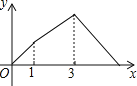
C. 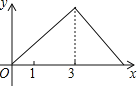 D.
D. 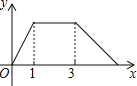
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com