

分析 (1)过P作PM∥AB,求出PM∥AB∥CD,根据平行线的性质得出∠A=∠APM,∠C=∠CPM,即可得出答案;
(2)根据平行线的性质得出即可;
(3)过P作PM∥AB,过Q作QN∥AB,求出AB∥PM∥QN∥CD,根据平行线的性质得出∠ABP=∠BPM=x,∠C=∠CQN,∠QPM=∠PQN,即可求出答案.
解答 解:(1)证明:过P作PM∥AB,
∴∠A=∠APM,(两直线平行,内错角相等),
∵PM∥AB,AB∥CD(已知),
∴PM∥CD,(平行于同一直线的两直线平行),
∴∠C=∠CPM( 两直线平行,内错角相等),
∵∠APC=∠APM+∠CPM,
∴∠APC=∠A+∠C(等量代换),
故答案为:两直线平行,内错角相等,平行于同一直线的两直线平行,∠CPM,两直线平行,内错角相等;
(2)∠A+∠P+∠Q+∠C=540°,
故答案为:540°;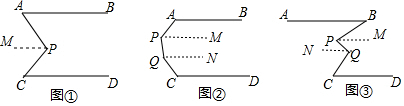
(3)m=x+z-y,
理由是:如图③,过P作PM∥AB,过Q作QN∥AB,
∵AB∥CD,
∴AB∥PM∥QN∥CD,
∴∠ABP=∠BPM=x,∠C=∠CQN,∠QPM=∠PQN,
∴∠C=∠CPQ-∠NPQ=∠CPQ-∠QPM=∠CQP-(∠BPQ-∠B)=z-(y-x)=x+z-y.
点评 本题考查了平行线的性质和判定,能正确作出辅助线是解此题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
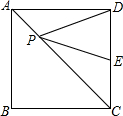 如图,在正方形ABCD中,AB=9,点E在CD边上,且DE=2CE,点P是对角线AC上的一个动点,则PE+PD的最小值是( )
如图,在正方形ABCD中,AB=9,点E在CD边上,且DE=2CE,点P是对角线AC上的一个动点,则PE+PD的最小值是( )| A. | 3$\sqrt{10}$ | B. | 10$\sqrt{3}$ | C. | 9 | D. | 9$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
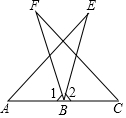 如图,已知AB=CB,BE=BF,点A,B,C在同一条直线上,∠1=∠2.
如图,已知AB=CB,BE=BF,点A,B,C在同一条直线上,∠1=∠2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com